GSSHA Primer
Contents
- 1 Overview
- 1.1 History
- 1.2 Description
- 1.3 Process simulated
- 1.3.1 Precipitation distribution
- 1.3.2 Snowfall accumulation and melting
- 1.3.3 Precipitation interception
- 1.3.4 Infiltration
- 1.3.5 Green and Ampt
- 1.3.6 Multi-layer Green and Ampt
- 1.3.7 Green and Ampt with redistribution
- 1.3.8 Richards’ equation
- 1.3.9 Overland flow routing
- 1.3.10 Channel routing
- 1.3.11 Lake and Detention Basin Routing
- 1.3.12 Wetland Hydraulics
- 1.3.13 Evapotranspiration
- 1.3.14 Soil moisture in the vadose zone
- 1.3.15 Lateral saturated groundwater flow
- 1.3.16 Stream/groundwater interaction
- 1.3.17 Exfiltration
- 1.3.18 Subsurface Drainage
- 1.4 Applications
- 1.5 Modeling process
- 2 Watershed Delineation and Grid Construction
- 3 Building a Basic GSSHA Simulation
- 4 Additional Modeling Capabilities
- 5 Assigning Parameter Values to Individual Grid Cells
- 5.1 Index maps
- 5.2 Mapping tables
- 5.3 Assigning uniform parameters
- 5.4 Assigning spatially distributed parameters
- 5.4.1 Locating GIS data
- 5.4.2 Consistent Coordinate Systems
- 5.4.3 Elevation
- 5.4.4 Land use
- 5.4.5 Classification codes
- 5.4.6 Soils
- 5.4.7 Accessing the texture information
- 5.4.8 Using texture to create an index map
- 5.4.9 Assigning spatially distributed infiltration parameters based on soils
- 5.4.10 Adjusting infiltration values based on land cover
- 5.4.11 Mapping to the Grid
- 6 Lake and Channel Routing
- 7 Embankments
- 8 Wetlands
- 9 Spatially and Temporally Varying Rainfall
- 10 Long-term Simulations
- 11 Modeling the Unsaturated Zone with Richards' Equation
- 12 Modeling Two-dimensional, Saturated, Lateral Groundwater Flow
- 13 Running GSSHA
- 14 Post-Processing
- 15 References
Overview
GSSHA: Gridded Surface Subsurface Hydrologic Analysis
What is GSSHA? Gridded Surface Subsurface Hydrologic Analysis (GSSHA) is a physics-based, distributed, hydrologic, sediment and constituent fate and transport model. Features include two dimensional (2-D) overland flow, 1-D stream flow, 1-D infiltration, 2-D groundwater, and full coupling between the groundwater, shallow soils, streams, and overland flow. Sediment and constituent fate and transport are simulated in the shallow soils, overland flow plane, and in streams and channels. GSSHA can be used as an episodic or continuous model where soil surface moisture, groundwater levels, stream interactions, and constituent fate are continuously simulated. The fully coupled groundwater to surface-water interaction allows GSSHA to model basins in both arid and humid environments.
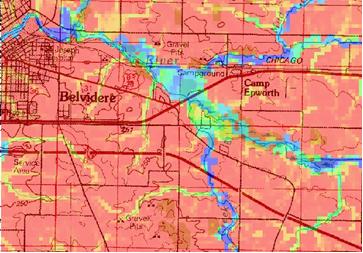
Flooding outside of Belvidere, IL.
What can GSSHA do?
GSSHA functions as a general hydrologic, hydraulic, sediment transport and chemical fate and transport model. The spatially explicit nature of the model makes it uniquely qualified for analysis of inherently distributed problems, such as sediment and non-point source pollution assessment and abatement. Because the model is a fully coupled surface water and groundwater model it can be used in a variety of environments, from arid desert regions in the west to humid forest on the eastern shore. Coupling of the watershed hydrology to the river and reservoir portions of the code allows it to be used for complete assessment of sediment fate, from erosion on the uplands to deposition in the reservoir. The fate of associated pollutants can also be tracked through the coupled system. Because the model is scalable it can be applied to large scale issues, such as the management of military training lands, and to small studies where detail at the street level is critical, such as urban flooding. The continuous hydrology model provides soil moisture predictions that can be used to asses fire threat, irrigation needs, and effects on natural systems. The physics based nature of the model makes it applicable for the analysis of future conditions, such as land use changes, and management scenarios, wetland restoration, BMPs, etc., for flood control, sediment transport, and pollutant transport. Utilizing unique boundary conditions this capability can be extended to simulation of coastal flooding due to storm surge. These are just a few ways that GSSHA has been and can be used.
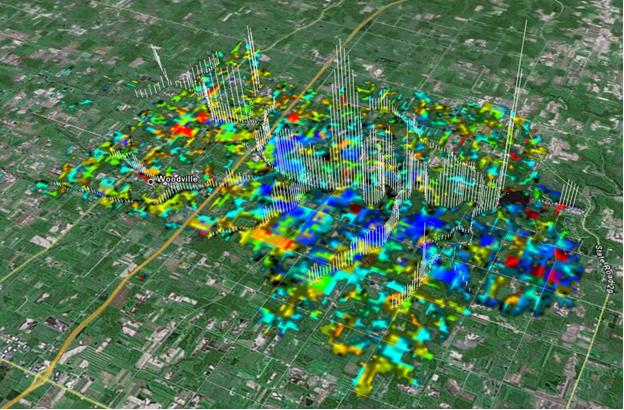
Mass of a dissolved nutrient, in-field (colors) and in-stream (lines). Woodville, WI. Note the reservoir (teal arrow, Spring Reservoir) in the simulation.
Where do I learn more?
- The GSSHA wiki is the best source of information, executables, training materials, and all other things GSSHA.
- The GSSHA information sheet can be found here: * GSSHA Information Sheet.
- The GSSHA storyboard can be found here: * GSSHA storyboard
- The ERDC CHL website on GSSHA can be found here http://chl.erdc.usace.army.mil/gssha
- Contact: Dr. Charles W. Downer – charles.w.downer@usace.army.mil
History
The GSSHA model is a significant reformulation and enhancement of the CASC2D model (Ogden and Julien 2002). The CASC2D runoff model originally began with a two-dimensional (2-D) overland flow routing algorithm developed and written in a programming language (APL) by Prof. P. Y. Julien, Colorado State University. The overland flow routing module was converted from APL to FORTRAN by Dr. Bahram Saghafian, then at Colorado State University, with the addition of Green & Ampt infiltration and explicit diffusive-wave channel routing (Julien and Saghafian 1991; Saghafian 1992; and Julien, Saghafian, and Ogden 1995). The FORTRAN code was reformulated, significantly enhanced, and rewritten in the C programming language by Dr. Saghafian at the U.S. Army Construction Engineering Research Laboratories. This version, named r.hydro.casc2d, was part of the Geographic Resources Analysis Support System/Geographic Information System (GRASS)/(GIS) for hydrologic simulations (Saghafian 1993). Work began in 1995 to reformulate CASC2D with the addition of continuous simulation capabilities and ability to interface with the Watershed Modeling System (WMS) graphical user interface developed by the Environmental Modeling Research Laboratory (EMRL) at Brigham Young University (BYU). This version, known as CASC2D for WMS, is distinguished from its predecessors by the addition of a number of new capabilities, numerous improvements and bug fixes, and a more stringent copyright. Johnson (1997) added overland sediment transport. Development of the CASC2D model for WMS by the Department of Defense (DoD) ended with version 1.18b, which has been the working distributed hydrologic model for the DoD (Downer et al. 2002a). CASC2D Ver. 1.18b is linked with WMS 5.1 as described by (BYU 1997a and 1997b).
While developed from the CASC2D model, the GSSHA model is inherently different in that it extends the capability of the model to simulate runoff mechanisms other than infiltration excess. Also, input of parameters for the GSSHA model is significantly different from the methods employed for CASC2D. The GSSHA model is backwards compatible with CASC2D Ver. 1.18b data sets. CASC2D Ver. 1.18b, and thus GSSHA, is not necessarily compatible with prior versions of CASC2D data sets. Also, WMS no longer supports the CASC2D input format, which is based on providing parameter values for every grid cell through a number of floating point GRASS ASCII format maps. When trying to utilize old CASC2D data sets, make sure they conform to the standards described in the GSSHA User’s Manual.
Version 2.0 of GSSHA has a new stream formulation and the ability to model wetlands, lakes, and detention basins.
Description
GSSHA is a physically based, distributed-parameter, structured grid, hydrologic model that simulates the hydrologic response of a watershed subject to given hydrometeorological inputs. Major components of the model include spatially and temporally varying precipitation, snowfall accumulation and melting, precipitation interception, infiltration, evapotranspiration, surface runoff routing, simple lake storage and routing, unsaturated zone soil moisture accounting, saturated groundwater flow, wetland peat layer hydraulics, overland sediment erosion, transport and deposition, in-stream sediment transport, and overland contaminant transport, and uptake. In GSSHA, each process has its own time-step and an associated update time. During each time-step, the update time of each process selected by the user is checked against the current model time. When they coincide, the process is updated, and updated information from that process is transferred to dependent processes. The update time or time-step of dependent processes may be modified as part of the process update. This formulation permits the efficient simultaneous simulation of processes that have dissimilar response times, such as overland flow, evapotranspiration (ET), and lateral groundwater flow. This scheme also allows an integrated solution of processes coupled through boundary conditions and flux exchanges.
Process simulated
GSSHA is a process-based model. Hydrologic processes that can be simulated and the methods used to approximate the processes with the GSSHA model are listed in Table 1. For several processes, there are multiple solution methods. A brief description of the processes and solution methods is presented. To obtain detailed information about the processes and methods, please refer to the GSSHA User’s Manual (Downer and Ogden in preparation).
| Process | Description | ||||
|---|---|---|---|---|---|
| Precipitation distribution |
| ||||
| Snowfall accumulation and melting | Energy balance | ||||
| Precipitation interception | Two-parameter empirical | ||||
| Overland water retention | Specified depth | ||||
| Infiltration |
| ||||
| Overland flow routing |
2-D lateral diffusive wave
| ||||
| Channel routing | 1-D longitudinal, explicit, up-gradient, diffusive wave | ||||
| Lake storage and routing | Level pool routing | ||||
| Wetland peat layer hydraulics | Mixed Darcian and Manning's flow. | ||||
| Evapotranspiration |
Deardorff (1977) Penman-Monteith with seasonal canopy resistance | ||||
| Soil moisture in the Vadose zone |
Bucket, 1-D vertical Richards’ equation (RE) | ||||
| Lateral saturated groundwater flow | 2-D vertically averaged | ||||
| Stream/groundwater interaction | Darcy’s law | ||||
| Exfiltration | Darcy’s law | ||||
| Subsurface Drainage | SUPERLINK |
Table 1. Process and Approximations Techniques in the GSSHA Model. (G&A – Green and Ampt (1911), GAR – Green and Ampt with Redistribution (Ogden and Saghafian 1997), RE – Richards’ equation (Richards 1931), ADE – alternating direction explicit, ADE-PC – alternating direction explicit with prediction-correction (Downer et al. 2002b)
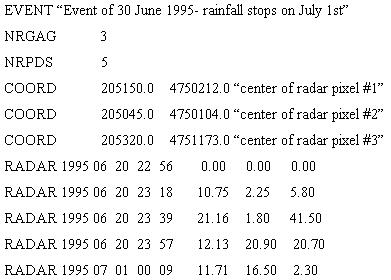
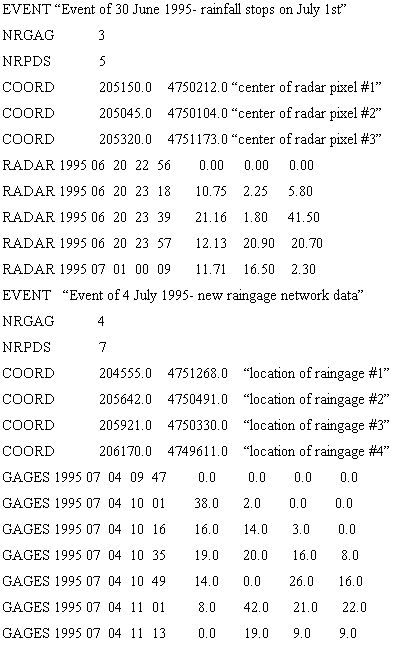
Precipitation distribution
In GSSHA, precipitation may be spatially distributed over the watershed by specifying a number of rain gages in the rainfall input file. Precipitation is distributed between the gages using either Thiessen polygons or an inverse distance square weighted method. Precipitation at each gage may vary in time, and non-uniform time increments may be used.
Snowfall accumulation and melting
Precipitation will automatically be treated as snowfall any time long-term simulations are conducted and the dry bulb temperature is below 0° C. Any accumulated snowfall is treated as a one-layer snowpack that melts as a result of heat sources including: non-frozen precipitation, net radiation, heat transferred by sublimation and evaporation, and sensible heat transfer as the result of turbulence.
Precipitation interception
Interception is the process of vegetation capturing precipitation and preventing it from reaching the land surface. Interception is modeled in GSSHA using an empirical two-parameter model that accounts for an initial volume of water that vegetation can hold plus the fraction of precipitation captured after the initial volume of water has been satisfied. The fate of intercepted water is not accounted for in GSSHA. The rainfall intercepted by vegetation is assumed to evaporate.
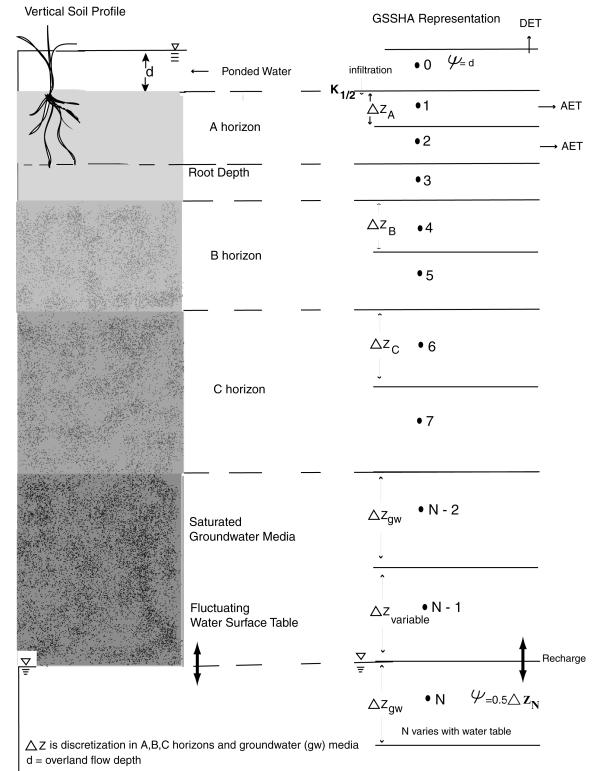
Infiltration
Infiltration is the process whereby rainfall and ponded surface water seep into the soil because of gravity and capillary suction. In GSSHA there are two general methods used to simulate infiltration. These are the Green and Ampt (1911) model and the Richards’ equation (1931) models. There are also two extended Green and Ampt models, making a total of four infiltration options to chose from.
Green and Ampt
The use of all the Green and Ampt based methods is limited to conditions where infiltration excess, or Hortonian runoff (Horton 1933), is the dominant stream flow producing mechanism. In the Green and Ampt model of infiltration, water is assumed to enter the soil as a sharp wetting front. Precipitation on initially dry soil is quickly infiltrated because of capillary pressure. As rainfall continues to fall and the ground becomes saturated, the infiltration rate will decrease until it approaches the saturated hydraulic conductivity of the soil.
Multi-layer Green and Ampt
The Green and Ampt model described assumes an infinitely deep, homogeneous, soil column. The GSSHA model also allows the user to specify Green and Ampt infiltration into soils with three defined layers. Changes in the hydraulic properties resulting from layering in the soil column always results in reduced infiltration capacity.
Green and Ampt with redistribution
When conducting long-term simulations, the Green and Ampt infiltration with redistribution (GAR) can be used (Ogden and Saghafian 1997). With GAR, multiple sharp wetting fronts can be simulated, and the water is redistributed in the soil column during non-precipitation periods.
Richards’ equation
Richards’ equation is currently the most complete method to compute soil water movement including hydrologic fluxes such as infiltration, actual evapotranspiration (AET), and groundwater recharge. The use of Richards’ equation is not limited to Hortonian runoff calculations. Richards’ equation is a partial differential equation (PDE) that is solved using finite difference techniques. In GSSHA three soil layers, each with independent parameters for each soil type and layer, are specified. Because the Richards’ equation is highly nonlinear, finding a solution can be difficult and time-consuming when Richards’ equation is used to simulate the highly transient conditions often found in hydrology, such as sharp wetting fronts and fluctuating water table. The GSSHA model employs powerful, mass conserving methods of solving the Richards’ equation and has been capable of simulating both soil moistures and associated hydrologic fluxes when the proper spatial discretization is employed (Downer 2002).
Overland flow routing
Water on the soil surface that neither infiltrates nor evaporates will pond on the surface. It can also move from one grid cell to the next as overland flow. The overland flow routing formulation is based on a 2-D explicit finite volume solution to the diffusive wave equation. Three different solution methods are available: point explicit, alternating direction explicit (ADE), and ADE with prediction-correction (ADE-PC). Through a step function, a depression depth may be specified. No water is routed as overland flow until the depth of water in the cell exceeds the depression depth. This depression depth represents retention storage resulting from microtopography.
Channel routing
When channel routing is specified, overland flow that reaches a user-defined stream section enters the stream and is routed through a 1-D channel network until it reaches the watershed outlet. Channel routing in GSSHA is simulated using an explicit solution of the diffusive wave equation. This simple method has several internal stability checks that result in a robust solution that can be used for subcritical, supercritical, and transcritical flows.
Lake and Detention Basin Routing
Lakes and detention basins are simulated as a lumped volume that can grow over the spatial domain of the model. As the lake grows or shrinks the connected streams shorten or lengthen as appropriate.
Wetland Hydraulics
Wetlands are simulated through a conceptual model that includes lateral darcian flow through a peat layer, vertical infiltration through a peat layer, and a mixed darcian and manning's flow through the overlying vegetation.
Evapotranspiration
Evapotranspiration (ET) is the combined effect of evaporation of water ponded on the soil surface and contained in the soil pores, as well as the transpiration of water from plants. GSSHA uses evapotranspiration to track soil moisture conditions for long-term simulations. Evapotranspiration can be modeled using two different techniques, the Deardorff (1977) and Penman-Monteith (Monteith 1965 and 1981). The Deardorff method is a simplified method used for formulations involving only bare soil. The Penman-Monteith method is a more sophisticated method used for vegetated areas.
Soil moisture in the vadose zone
During long-term simulations, the soil moisture in the unsaturated, or vadose, zone can be simulated with one of two methods: a simple fixed soil volume accounting method (Senarath et al. 2000) (bucket method), or simulation of soil moisture movement and hydrologic fluxes using Richards’ equation (Downer 2002). Evaporative demand is supplied to either method by the ET calculations.
Lateral saturated groundwater flow
Where groundwater significantly affects the surface water hydrology, saturated groundwater flow may be simulated with a finite difference representation of the 2-D, lateral, saturated groundwater flow equations. The saturated groundwater finite difference grid maps directly to the overland flow grid. The saturated groundwater zone resides below the unsaturated zone, which may be represented with either the GAR model or the Richards’ equation model. When simulating saturated groundwater flow, the additional processes of stream/channel interaction and exfiltration may occur.
Stream/groundwater interaction
When both saturated groundwater flow and channel routing are being simulated, water flux between the stream and the saturated groundwater can be simulated. By specifying that both overland flow and saturated groundwater flow grid cells containing stream network nodes be considered as river flux cells, water will move between the channel and the groundwater domain based upon Darcy’s law.
Exfiltration
Exfiltration is the flux of water from the saturated zone onto the overland flow plane. You may have seen a seep at a change in slope on a hillside. This seepage is exfiltration. Exfiltration occurs when the water table elevation exceeds that of the land surface. Fluxes to the land surface are computed using Darcy’s law.
Subsurface Drainage
Subsurface drainage networks can be simulated in GSSHA using the SUPERLINK model. Surface inlets and subsurface tile drains can be simulated. Drains and tiles can discharge to the overland flow plane or to channeles. Multiple connected or unconnected networks can be simulated.
Applications
GSSHA accounts for the following conditions that may be encountered when simulating watershed hydrology:
- Spatial variability of soil textures, land use, and vegetation that may affect parameter values needed to simulate important hydrologic processes.
- Spatial and temporal variability of precipitation.
- Snowfall accumulation and melting.
- Drainage network of arbitrary shape and cross sections.
- Effect of soil moisture on infiltration and runoff.
- Effect of water table on soil moisture, infiltration, and runoff.
- Gaining and losing streams.
- Hortonian runoff.
- Saturated source areas.
- Exfiltration.
- Wetland peat hydraulics.
- Lake storage and routing.
It has been verified that GSSHA, and/or the methods taken from CASC2D and employed in GSSHA, can be used to simulate the following types of hydrologic variables:
- Stream discharge in Hortonian basins (Doe and Saghafian 1992; Ogden et al. 2000; Senarath et al. 2000; Downer et al. 2002a)
- Stream discharge in non-Hortonian and mixed runoff basins. (Downer 2002; Downer et al. 2002b)
- Soil moistures in Hortonian basins. (Downer 2002).
- Sediment discharge in Hortonian basins (Johnson 1997)
Modeling process
Application of GSSHA requires the creation of a variety of input files and grid data (or maps). GSSHA has been coupled with WMS in an attempt to minimize the time required to create the needed inputs. WMS is also intended to aid in model conceptualization and analysis of results. The basic parts of the modeling process are watershed delineation and computational grid construction, selection of processes to model, parameter assignment, channel routing assignment, running the model, and post-processing. The GSSHA User’s Manual (Downer and Ogden in preparation) provides detailed information on the modeling process.
Grid construction
GSSHA is a finite difference based model and requires a 2-D grid representation of the watershed being modeled. Construction of this grid is the first step in the development of a GSSHA model. WMS has a variety of tools that can be used for watershed delineation and grid generation from digital elevation data as well as data exported from the GRASS or Arc/Info GISs.
Process selection
Once the grid is constructed, the processes to be simulated must be selected based on the needs of the study. The processes to be simulated are selected in the GSSHA Job Control. It is best to start with a simple model with few processes and proceed to build more complicated models with several processes. The GSSHA User’s Manual (Downer and Ogden in preparation) should be consulted for more information on which processes are appropriate for which studies.
Model parameter assignment
Once the grid has been created and processes selected, model parameters governing the execution of GSSHA must be assigned. Model parameters include global variables such as simulation time and time-step, as well as the distributed parameters needed to simulate processes such as interception, infiltration, and overland flow routing. WMS facilitates global parameter assignment with dialog boxes and distributed-parameter assignment with the use of index maps and the mapping tables.
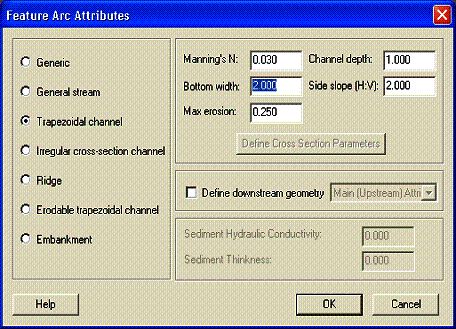
Channel routing
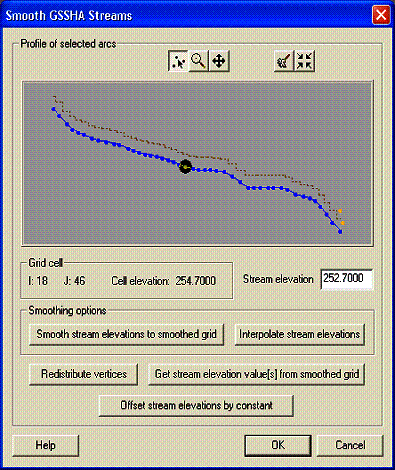
Larger watersheds normally require that the 1-D channel routing option in GSSHA be used. The channel routing method is an explicit diffusive-wave approximation of the St. Venant equations. The channel network is described with a series of links and computational nodes. A link can be a channel segment, hydraulic structure, or lake. WMS feature arcs are used to create the channel links and assign cross-sectional parameters to the links. In order to couple the channel routing with surface runoff, GSSHA must know which grid cells “contain” stream nodes. When WMS creates the appropriate input files, grid cells beneath the stream arcs are identified and the portion of each stream node in the each cell is written to the grid stream file. WMS has several tools for creating, numbering, and assigning parameters to the channel links and nodes.
Running GSSHA
Once all necessary input for a GSSHA simulation has been prepared, the GSSHA model is run. GSSHA is a stand-alone program that can be executed from the command line or through the WMS interface.
Post-processing
Results from successful GSSHA simulations may be viewed in WMS. The optional output created by GSSHA can include gridded time series of maps of a number of variables including: surface water depth, infiltration rate, cumulative infiltrated depth, spatially varied rainfall, soil moistures, groundwater heads, and others. Time series output of discharge and depth can be produced at all nodes in the channel network in this new format. WMS has capabilities to contour, shade, and animate the results for the entire 2-D grid and all along the stream network. Additionally, 2-D plots of any result variable versus time can be generated for any location in the grid or on the stream network. Post-processing techniques are used to help the user determine if a solution is reasonable or if further model modification is necessary.
Watershed Delineation and Grid Construction
The primary input files for a GSSHA rainfall/runoff simulation are the 2-D finite difference grid and its accompanying surface elevations. The grid is a rectangular area that covers the extents of the watershed. Individual cells whose centroid are within the watershed boundary are flagged as “active” (a value of “1” in the watershed mask), and cells outside the boundary are flagged as “inactive” (a value of “0” in the watershed mask). WMS can be used to automatically delineate a watershed boundary from digital elevation data and then construct a finite difference grid with the appropriate active and inactive flags set for individual cells.
In this chapter you will learn where to locate digital elevation data that can be used for automated basin delineation and assignment of surface elevations for the finite difference grid. You will also learn the basic processes used by WMS to delineate the watershed boundary and construct a grid.
Obtaining DEM data for watershed delineation
The United States Geological Survey (USGS) has converted their topographic maps into digital elevation model (DEM) files. These files represent the land surface as a matrix (grid) of elevation values at a given space (resolution) apart. The most commonly used maps are the 1:24,000 series that are commonly found in a 30-m resolution, with many areas now being converted to a 10-m resolution. In addition, the 1:250,000 map series has also been converted into 3 arc-second (approximately 90 m) resolution DEMs. Both DEM classes have been distributed by the USGS for a number of years. More recently free downloads are available from the World Wide Web (www). Many other local, state, and Federal agencies warehouse and deliver these DEM products. The EMRL at BYU has developed a single website that contains links to some of the most common and easy to use websites for free downloading of DEM data. This website is hosted at:
http://www.xmswiki.com/index.php?title=GSDA:GSDA
In addition to DEM data, this site also contains resources for locating, downloading, and preparing land use, soil textural classification, and image data. Each topic contains basic information, frequently asked questions, and detailed instructions for obtaining and preparing the data to be used in WMS.
A new exciting feature of WMS is the use of web services to automatically retrieve data. The USGS hosts the National Elevation Dataset on the internet. The information contained in the web site can be directly downloaded and accessed by WMS from within WMS.
DEM File Formats
The USGS has two different file formats. Historically, quadrangle map DEMs have been stored in a single file using what is often referred to as the “USGS Format.” In recent years, the Federal Geographic Data Committee (FGDC) has developed standards for sharing spatial data and most DEMs have been converted to this format, referred to as the “SDTS Format.” WMS can import either format, but the old-style USGS format is a little easier to work with. The SDTS is a format defined for vector as well as raster (grid) data. Multiple files are required to define the elevation grid with the SDTS format. In the case of DEMs, many of these required files are blank or small. The USGS DEMs often are named with a “. dem” extension while the SDTS DEM files will contain a “. ddf” extension. When reading the SDTS DEM, any of the “.ddf” files may be specified for the file. WMS will automatically extract the needed information from the various files.
Besides the two USGS file formats, the Arc/Info ASCII grid is another commonly used format by many GIS systems. If you are trying to obtain data stored in Arc/Info grid files, you must have the grid converted to ASCII, as the binary file format is proprietary to Environmental Systems Research Incorporated (ESRI) and unreadable by WMS. WMS also supports the DTED and GRASS grid file formats.
Watershed delineation
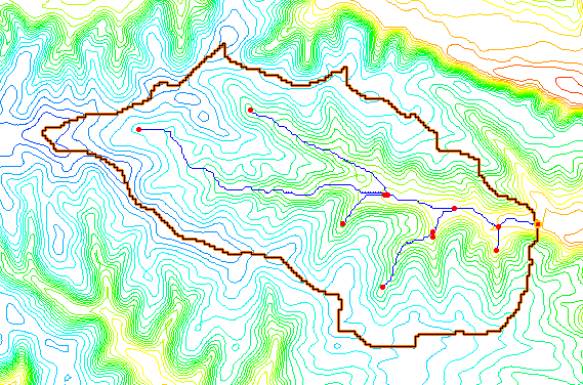
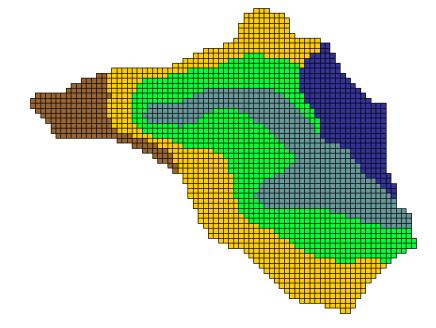
While it is possible to manually create a finite difference grid and set the active and inactive regions, it is not recommended. Since the DEM (or other elevation data) will be used to assign elevations to the grid cells, it is good practice to use the elevation data to automatically create a watershed boundary. You can then use that boundary (a polygon, as shown in Figure 1) to construct a grid that covers the watershed extents and automatically assigns cells within the boundary as active, and cells beyond as inactive.
WMS provides three methods of automated watershed delineation, namely via DEMs, TINs, and feature objects. An overview of each is given here. A broader overview can be found in the WMS reference file under the Introduction chapter, with more detailed instructions in the individual chapters. The simplest and best way to create the watershed boundary is from the DEM. Additional methods can be employed if you do not have access to the required DEM data.
Basin delineation with DEMs
DEM data can be used in WMS to automatically delineate basin boundaries and define stream networks. Typically a USGS DEM (multiple quadrangles can be tiled together) is imported. Any gridded elevation data set can be used providing it is in one of the formats readable by WMS. The United States Department of Agriculture (USDA) program TOPAZ (Martz and Garbrecht 1992) is launched from WMS to define flow directions and flow accumulations for each DEM cell. This information is used to trace and convert the stream networks and basin boundaries to lines and polygons of the WMS drainage coverage. The polygon and stream network shown in the Figure 1 were delineated in WMS using this method. More details about basin delineation with DEMs can be found in the WMS help file (Nelson 2003).
Basin delineation with TINs
Triangulated Irregular Networks (TINs) can also be used to delineate a watershed boundary that will be used for GSSHA models. A TIN is another form of elevation data, but rather than being organized as a grid, with rows and columns of elevations with equal spacing between, it is a network of triangles formed from scattered elevation points. TIN data are much less common than DEM data and slightly more complicated to work with. When using the TIN method for watershed delineation in WMS, you should convert the resulting boundaries and stream network to feature objects using the “Drainage Data-> Feature Objects command. Details on the use of TINs for automated watershed delineation can be found in the WMS help file.
Basin delineation with feature objects
If you have an existing watershed boundary and stream network already defined in a GIS or CAD environment, then it is possible to import these data in WMS as a drainage coverage and use the imported feature arcs directly to create the GSSHA grid and channel data. However, elevation data are still required to interpolate surface elevations to the resulting GSSHA grid. When using an existing watershed boundary, you should use caution because, unlike the DEM method where the boundaries and streams are defined directly from the elevations, the streams and boundary of the imported data may not coincide with the interpolated elevation data. This can result in elevation errors in overland flow grid cells and channel nodes, leading to numerical instability in the GSSHA model. The elevations in the resulting grid may need to be edited on a cell by cell basis. Further details on the use of feature objects are provided in the WMS Help File.
Grid sizes
In general, the higher the resolution of the finite difference grid (smaller grid cells), the more accurate the solution will be. While theoretically the number of grid cells that can be used for GSSHA modeling is unlimited, there are some practical limitations. In order to define all model parameters, approximately 3,500 bytes of memory are required for each grid cell. This means that one megabyte of RAM is required for each 300 grid cells of a GSSHA simulation. In addition to the amount of memory, the time to display and work with the model inside of WMS and the time required for the GSSHA simulation to run will increase.
The issue of appropriate grid sizes has not been adequately answered to date. Several research papers address the range of applicability of the diffusive wave form of the equations of motion that are used for overland flow routing in GSSHA. However, the picture is complicated by the difficulty in including the effects of microtopography on runoff routing. Given this fact, the use of any physically based routing technique is merely an approximation of reality. GSSHA has been successfully used with grid sizes ranging from 30 to 1,000 m (~100 ft to 3,280 ft). However, experience by the GSSHA developers has shown that grid sizes smaller than 200 m (660 ft) produce more robust calibrations. Downer et al. (2002b) discuss how grid size should be sufficiently small to capture the essential features in the study watershed. In general, the philosophy of distributed hydrology is that “smaller is better” provided that the problem remains computationally feasible and the quality of the data warrants the use of small grid sizes.
Constructing a grid
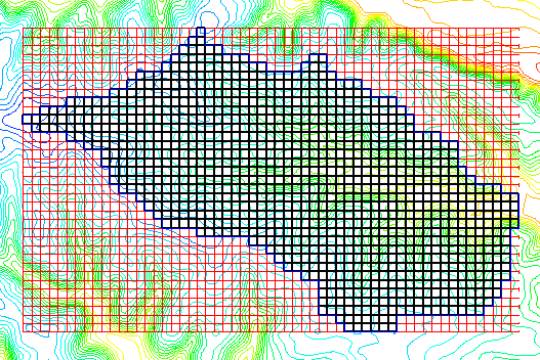
Once a boundary feature polygon has been defined by one of the methods described above, a 2-D grid can be created in WMS using the Create Grid command in the Feature Objects menu. WMS will then prompt you for the grid size and fill the interior of the rectangle that just bounds the watershed. Each grid cell is flagged as being inside the watershed (active) or outside the watershed (inactive) according to the location of the centroid of each grid cell. The results of a typical grid generation are shown in Figure 2.
For more information on how to use this command, please see the WMS Help File. This grid is the heart of the GSSHA model and defines the watershed mask (grid cells within the watershed) and elevation map required to run GSSHA.
Editing the grid to correct elevation errors
Pre-Processing:Editing the grid to correct elevation errors
Conclusions
The basic process used in WMS to create a grid is to first delineate the watershed boundary and streams from a DEM and convert the results to a bounding polygon for the watershed. This bounding polygon is then “filled” with grid elements of the appropriate size for the planned simulation, and elevations for grid cell centers are interpolated from the original DEM. WMS provides multiple options for creating the bounding polygon, but the recommended method is to use a DEM. WMS supports both USGS file formats as well as Arc/Info ASCII grid files.
The size of grid cells used for a GSSHA simulation will vary depending on the area of the watershed and objectives of the simulation, as well as computing resources. Inevitably some of the grid cells will need to have elevations adjusted to create more “natural” and numerically stable overland flow. There are a few options in WMS to help identify and mitigate problem cells. The need to edit grid cells is most easily identified by running a basic simulation to examine areas on the grid that pond excessively. Setting up and running a basic simulation is the content of the next chapter.
Building a Basic GSSHA Simulation
A complete GSSHA simulation may include temporally and spatially varying rainfall for multiple events over an extended period, distributed roughness parameters, infiltration modeling with distributed parameters, channel routing, and saturated groundwater flow with stream interaction. However, such a simulation is built in pieces, not all at once. A simple simulation is constructed, problems are corrected, and then additional processes or inputs are added, one at time. The key is to successfully build a simple simulation, and then build upon your success.
The most basic simulation is built through four steps:
- Assigning elevations to each cell, as described in Chapter 2.
- Assigning the values of a limited number of global parameters.
- Describing the uniform rainfall event.
- Assigning uniform value of overland flow roughness.
Once this simple simulation works, processes or complexities, as described in the following chapters, are added. The information in this primer is presented in the order that complexities should be added. The new simulation, with added complexity, should be tested before adding more complexity to the simulation. This process of building a simulation is described in detail in the Building a Model chapter in the GSSHA User’s Manual.
The global parameters of a simulation refer to the input control and other parameters not assigned on a cell-by-cell basis; e.g., the numerical method for computing overland flow, the computational time-step and total simulation time, and whether to activate certain model options such as channel routing, long-term simulations, infiltration, evapotranspiration, groundwater interaction, etc.
To have WMS allocate the memory required for development and storage of GSSHA model parameters, you must first initialize a simulation. This is usually done when creating a grid, because WMS prompts the user whether or not to do so. However, the simulation parameters can be initialized or deleted using the identified buttons in the GSSHA Job Control Parameters dialog. Data necessary to run a GSSHA simulation are determined based on the settings in the GSSHA Job Control Parameters dialog (Figure 3). A better description of the various options is provided in the next several sections.
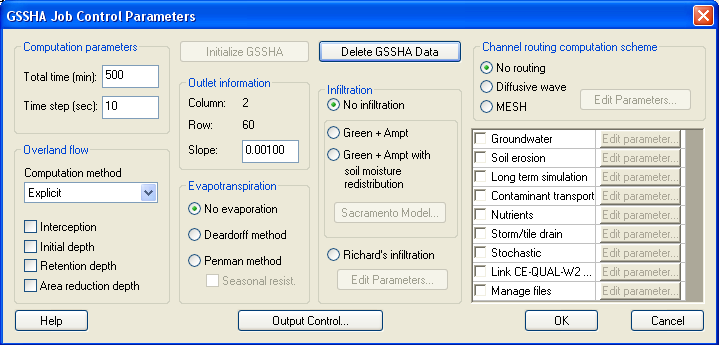
Global parameters
The global parameters of a simulation refer to the input control and other parameters not assigned on a cell-by-cell basis; e.g., the numerical method for computing overland flow, the computational time-step and total simulation time, and whether to activate certain model options such as channel routing, long-term simulations, infiltration, evapotranspiration, groundwater interaction, etc.
To have WMS allocate the memory required for development and storage of GSSHA model parameters, you must first initialize a simulation. This is usually done when creating a grid, because WMS prompts the user whether or not to do so. However, the simulation parameters can be initialized or deleted using the identified buttons in the GSSHA Job Control Parameters dialog. Data necessary to run a GSSHA simulation are determined based on the settings in the GSSHA Job Control Parameters dialog (Figure 4). A better description of the various options is provided in the next several sections.

Total time
The total time parameter sets the total simulation time for a model in minutes. If the falling limb of the discharge hydrograph is of particular interest, the total simulation time must be set to a value greater than total rainfall duration plus the expected recession time.
The total time is used only for single-event simulations. During long-term simulations, the total time is not used because the simulation time is determined from the rainfall and hydrometeorological input files.
Time-step
The time-step (Dt) is the duration of the computational time-step, in seconds. The time-step is a critical variable in determining the wall clock execution time for a simulation. Typical time-steps for GSSHA simulations range from 20 sec up to 5 min. For particularly hard problems, the time-step may need to be very short, 10 sec, 5 sec, or even less. One second (1 sec) is the smallest permissible time-step.
Note that the overall model time-step must be less than and divisible into the smallest increment of time in the rainfall file. For example, for 1-min rainfall data the maximum time-step is also 1 min. Other permissible values would be 30, 20, 10, 5, 2, and 1 sec. If saturated groundwater flow is being simulated, then the overall model time-step must also be equal to or less than, and integer divisible into, the groundwater time-step.
The general rule for overland routing is that shorter time-steps must be used for higher intensity storms, finer horizontal grid resolution (grid spacing, Dx), steeper watershed slopes, larger watershed areas, and smoother surfaces. Stability of the explicit routing routines depends in part upon the Courant number. The Courant number is a dimensionless number that expresses the wave celerity, water velocity for steady flows, over the model celerity, Dt/Dx. For model stability, the Courant number must be less than 1.0; that is, water should not move more than one grid cell during a single time-step.
Shorter time-steps must be used when backwater effects are significant, which occurs mainly in flat areas. If the time-step is too long, the surface water depth in flat areas may show a checkerboard pattern, i.e., oscillations are observed in the water surface level. In such cases, the time-step should be decreased and the simulation repeated. Alternately the flat areas can be removed by editing the elevations.
Outlet information
When channel routing is not specified, information about which cell represents the watershed outlet and the slope of the land surface at the outlet must be defined. The outlet location is defined be creating a feature point in the desired cell and setting the type attribute to outlet. WMS will extract the I and J indices of the cell underlying the outlet point and feed that information to GSSHA. The outlet slope must be defined in the Job Control dialog. The bed slope is equal to the tangent of the angle that is made between the bed profile at the outlet and the horizontal plane. This slope is used to calculate the outflow overland discharge at the outlet based on a normal depth boundary condition. When channel routing is specified, the outlet of the catchment is defined by the location of the stream network and an outlet feature point need not be specified.
Units
GSSHA is entirely formulated in metric units. Therefore, the grid dimensions and elevations must be in meters. WMS can be used to convert grid dimensions and/or elevations from feet to meters. GSSHA outputs all results in metric units except for the flow values in the outlet hydrograph file (.otl file), which can be output in either metric (m^3/s) or English (cfs) units.
Defining a uniform precipitation event
Rainfall can be input in one of three formats:
- Uniform constant rainfall over the entire watershed.
- Single temporally varying rain gage.
- Multiple, temporally varying rain gages.
All rainfall types in GSSHA must be tied to a specific point in time by specifying the year, month, day, hour, and minute of each rainfall data point. The GSSHA Precipitation dialog in WMS allows you to specify the type of rainfall and enter the necessary data associated with the rainfall type (Figure 5).
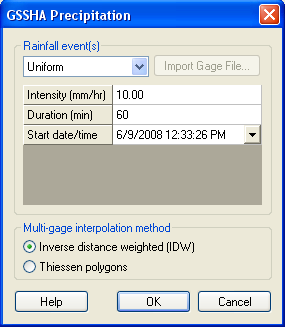
For a spatially uniform constant rainfall, the specified rainfall covers the entire basin for the specified period. The input parameters are:
- Rainfall Intensity - (mm/hr).
- Rainfall Duration - (minutes).
- Start Time.
- Year
- Month
- Day
- Hour
- Minute
Temporally and spatially varied precipitation is discussed in Chapter 9.
Describing overland flow
The computational method used to compute overland flow is selected in the GSSHA Job Control Parameters dialog from Overland flow sim. Three methods are available.
- Explicit – alternating direction, time varying version of the original point explicit method developed for CASC2D, as described by Julien and Saghafian (1991).
- ADE – alternating direction explicit (Downer 2002).
- ADE-PC – alternating direction explicit with prediction-correction (Downer 2002).
The default value is Explicit. The ADE and ADE-PC methods are described in the GSSHA User’s Manual. The explicit method has a variable time step that can adapt to computational needs. The ADE-PC method is very robust and may be employed when particularly difficult conditions are encountered. The ADE-PC method will often work when the other two methods will not. The additional computations in the ADE-PC method make it significantly slower than the other two methods, which require about the same wall clock time. Some experimentation may be required to determine which method will work best for a particular problem.
The following inputs are required in overland flow simulations in GSSHA.
- Land surface elevation.
- Land surface roughness.
The grid cell land surface elevations (determined from the DEM, as discussed in Chapter 2) and the surface roughness comprise the minimum input parameters that must be defined for a GSSHA surface runoff simulation.
The surface roughness represents the overland Manning’s roughness coefficient n. These values can be spatially distributed using an index map defined from vegetation cover and/or land use. Values of overland roughness coefficients based on vegetation coverage are presented by Engman (1986) and Ree, Wimberly, and Crow (1977), and summarized in the GSSHA User’s Manual (Downer and Odgen in preparation).
By using Manning’s resistance equation, it is assumed that the overland flow is turbulent flow over rough surfaces. Manning’s roughness coefficients are dimensionless. Assignment of parameter values to every grid cell is discussed in Chapter 5.
Verifying the basic model
For every new GSSHA model a basic simulation with uniform roughness should be run to determine the overall quality of overland flow. The minimum parameters that must be defined to run a basic simulation are surface roughness and rainfall. As described above, the time-step, total time, and outlet information must also be defined. The required steps are described below.
- In the GSSHA Job Control Parameters dialog, make sure that all optional processes (routing, sediment, infiltration, etc.) are turned off. Enter a value for total simulation time in minutes (a few hours) and a small time-step in seconds (5 to 10 sec). In the GSSHA Job Control Parameters dialog, select Output Control, toggle on Surface depth under the Data Set Map Options. Toggle on the ASCII map Type. Input a Write Frequency (minutes) such that maps of surface depth are written out every 15 to 30 min.
- For the uniform rainfall event, enter an intensity of 10 to 50 mm/hr and a duration of 60 to 120 minutes.
- Assign a uniform overland roughness coefficient, as described in Chapter 4, with a value of 0.05.
- Save the project and run GSSHA.
The model should run to completion and produce a hydrograph at the outlet. If the model runs but does not produce flow at the outlet, then either increase the total time of your simulation, your rainfall duration, or your rainfall intensity and rerun the model. Do this until there is output. The model may or may not run to completion as flow is produced.
If the model does run to completion, use the methods described in Chapter 14, Post-processing, to view the outlet hydrograph and the overland flow depth maps. These maps are useful for locating problem areas in the watershed and comparing areas of ponded water to independent topographic data. If water is ponded on the watershed at the end of the simulation (ponded water shows up as blue areas on the overland flow depth maps), compare these locations to topological maps and ensure that the ponded areas correspond to real depressions. If these areas should drain, you may have to go back and do more smoothing on the DEM or manually edit the values of elevation in the affected grid cells, as discussed in Chapter 2. Even if the ponding areas correspond to natural depressions, you may still wish to smooth the DEM or edit the grid elevations to drain these areas, as computation of overland flow with significant backwater effects requires a small time-step. Experience has shown that DEM smoothing has minimal effect on streamflow predictions.
If the overland flow routine crashes, information on problem areas will be printed to the screen and also to the run summary file. If the overland flow module will not run you can try to change the overland flow routing method to ADE-PC, reduce the time-step, or decrease the uniform rainfall intensity or duration. If the model will not run with a small time-step and the very stable ADE-PC overland flow routine, the depth maps should be consulted to identify potential problems in the watershed. The DEM may be smoothed using algorithms in the WMS software, or the elevations in the grid may also be manually edited. The information provided by GSSHA will tell you where to target editing of grid cell elevations. Zoom in on these identified problem areas; turn on the color fill contours, and display the grid cell elevations. You may have to remove flat spots, dams, or depressions that are causing the overland flow model to crash. If water is ponding along the edge of the watershed, these cells will either have to be removed from the grid or raised in elevation. Another potential solution to making the overland flow module run is to increase the grid size, which will reduce the Courant number and smooth the elevations in the model.
Determining an appropriate time-step
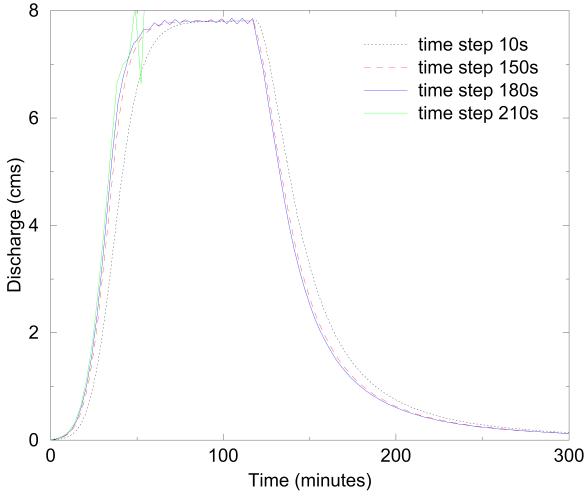
A good way to determine the appropriate time-step for a given problem is to conduct a temporal convergence study. Select from the study period a rainfall event of the highest rainfall intensity, or the one that produces the maximum discharge. Select a short time-step, 5 to 20 sec, and simulate the event. Write out the discharge hydrograph at small intervals, equal to the time-step. Increase the time-step and repeat. Continue increasing the time-step until the program crashes during execution. At this point, the upper limit of the time-step for your problem has been reached. Look at the hydrographs produced using the various time-steps. If the hydrograph begins to oscillate, normally near the peak, the time-step is too large. Eliminate any simulations that produce oscillations in the hydrograph.
There should now be a set of hydrographs produced by various time-steps. As the time-step is increased, the hydrograph shape may begin to change. A primary theory of the finite difference method is that the model results converge on the solution as the time-step decreases. Therefore, the hydrograph with the smallest time should be treated as the “correct” answer, and the other hydrographs should be judged against it. A simple visual comparison of the hydrographs is usually sufficient. Figure 6 shows the hydrographs produced from a test case with time-steps of 10, 150, 180, and 210 sec. At 150 sec, the hydrograph is significantly shifted from the 10-sec simulation. At 180 sec, oscillations appear. At 210 sec, the oscillations cause the model to crash. All these time-steps are too large. The simulation time-step may also be judged by the peak discharge, time of peak, and discharge volume information from the summary file. To decrease wall clock execution time, select the largest time-step that produces results equal to, within an acceptable error level, the results with the smallest time-step.
Additional Modeling Capabilities
As described in Chapter 1, there are many modeling options in GSSHA beyond the basic overland flow model described in Chapter 3. This chapter summarizes and describes the additional modeling options in GSSHA. More detailed descriptions of some modeling options are offered in following chapters, as needed.
The processes GSSHA simulates to predict stream flow may include overland flow, spatially and temporally varied rainfall, infiltration, and channel routing. It is typical to use the long-term model to conduct simulation calibration or to simulate extended events. Modeling of the unsaturated zone with Richards’ equation and saturated groundwater modeling may be required in areas where infiltration-excess runoff is not the predominate stream-flow producing mechanism. Sediment routing is an additional capability used in studies specifically designed to compute sediment loads.
Overland flow routing options
Capabilities:Overland flow routing options
Infiltration
GSSHA provides two basic methods and four different options for simulating infiltration. The two basic methods are the Richards’ equation, described in Chapter 11, and the Green and Ampt method (1911), as described below. Selection of Richards’ equation over one of the Green and Ampt methods actually results in the model operating quite differently, most notably during long-term simulations (Chapter 10).
There are three Green and Ampt methods; basic Green and Ampt (1911), Green and Ampt with Redistribution (GAR) (Ogden and Saghafian 1997), and multi-layer Green and Ampt (Downer and Ogden in preparation). The multi-layer Green and Ampt model is not currently supported by WMS, and the user is referred to the GSSHA User’s Manual for more information on this option.
In the Job Control dialog, one of four choices can be specified:
- No infiltration.
- Green & Ampt.
- Infiltration redistribution (Green & Ampt with redistribution).
- Richard’s infiltration.
If no infiltration method is specified, then no parameters need be defined. If Green & Ampt is chosen, then grid parameters of soil hydraulic conductivity, porosity, wetting front suction head (capillary head), and initial moisture content must be defined. If the infiltration with redistribution option is chosen, the pore distribution index and residual saturation must also be defined. Selection of Richards’ equation requires the user to specify both global parameters and distributed grid cell parameters, as described in Chapter 11.
Green & Ampt Infiltration
In the Green and Ampt model of infiltration, water on an overland flow grid cell resulting from precipitation, overland flow, or other sources is assumed to enter the soil as a sharp wetting front. The soil behind the front is assumed to be saturated. The soil ahead of the front is assumed to be at some uniform initial moisture. The wetting front is drawn into the soil because of gravity and soil capillary pressure. As the front moves into the soil column, the effect of the soil capillary head is reduced and infiltration slows, approaching the value of the saturated hydraulic conductivity.
Four soil property parameters are required for each cell:
- Saturated hydraulic conductivity (cm/hr).
- Wetting front suction head or capillary head (cm).
- Porosity - fraction of voids in the soil (m3/m3).
- Initial moisture content - initial fraction of water in the soil (m3/m3).
The first three parameters may be assigned based on an index map of soil textures. As the land use may also affect these parameters, it is typical to create a composite land use/soil texture index map to assign these parameters. In the absence of measured field data, the parameters may be estimated based on the soil textural classification. Tables of parameters can be found in Rawls, Brakensek, and Saxton (1982) and are summarized in the GSSHA User’s Manual (Downer and Ogden in preparation). Assignment of these parameters based on soil textural classification typically requires that one, some, or all of these parameters be adjusted during calibration.
The initial moisture content must be less than or equal to the porosity and should be greater than the residual water content. Estimation of the initial soil moisture is based on antecedent conditions in the watershed. The Green and Ampt method is highly sensitive to the value of initial moisture. Accurate initial moisture estimates are required. Initial moisture estimates may be determined from field measurements, satellite measurements, or may be provided by the GSSHA model when long-term simulations are conducted (Chapter 10). Senarath et al. (2000) demonstrate the dangers of using initial moisture as a calibration parameter in single event calibrations.
Redistribution
When GAR (Green & Ampt with Redistribution) is selected for modeling infiltration, soil pore water is redistributed during periods of no or low-intensity rainfall, and infiltration capacity recovers for the next burst of storm intensity. The technique used for storm hiatus and post-hiatus stages is based on the method by Smith, Corradine, and Melone (1993) with minor modifications (Ogden and Saghafian 1997). In this model, the Green & Ampt equation is used for post-hiatus stage, so the four Green & Ampt parameters (described above) must be specified. In addition, the pore size distribution index (dimensionless) and residual saturation (dimensionless) are required. Without field measurements, values for these parameters may also be estimated based on soil textural classifications and assigned from literature values, e.g. Rawls, Brakensek, and Saxton (1982) and summarized in the GSSHA User’s Manual (Downer and Ogden in preparation).
Richards’ Infiltration
When Richards’ equation is specified for simulation of infiltration, the movement of water in the soil is explicitly solved using Richards’ equation (Richards 1931). Detailed soil moisture profiles are calculated in each overland grid cell with infiltration calculated as a by-product of the solution. Richards’ equation requires many of the same parameters described above, in addition to global parameters related to the solution techniques used in the model. Richards’ equation and the proper assignment of parameters are described in detail in Chapter 11.
Channel routing options
One-dimensional channel routing can be coupled with overland flow routing by turning on the channel routing option. A channel network, complete with geometric cross sections and other parameters, must be defined. Details of defining channel routing parameters for GSSHA using WMS are discussed in Chapter 6.
Long-term simulations
Long-term simulations can be used to simulate multiple rainfall events that occur over an extended time period. The effects of wetting and drying of the soils in the watershed are simulated. Long-term simulations require many additional inputs as detailed in Chapter 10.
Subsurface
Subsurface simulations can be performed to simulate the lateral flow of saturated groundwater movement and interactions with surface water. The 2-D free surface equation (Pinder and Bredehoeft 1968) is solved using finite difference techniques (Trescott and Larson 1977; Downer 2002). Selecting this option requires the assignment of appropriate boundary conditions and parameters to define the groundwater media. Details of simulating saturated groundwater are discussed in Chapter 12.
Assigning Parameter Values to Individual Grid Cells
As described in the preceding chapters, the simulation of many processes requires that parameter values be assigned to every cell in the active watershed grid. GSSHA can accept parameter values for every cell as a specified uniform value, as a GRASS ASCII map with a different value for every cell, or as tabled values referenced to index maps.
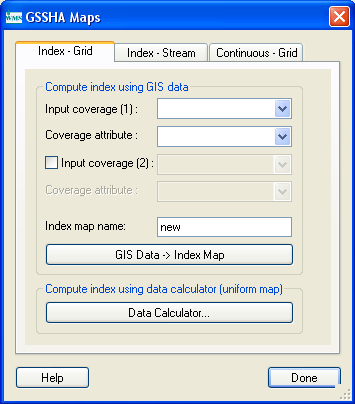
In WMS, parameters are assigned to cells by using the mapping tables and index maps. Index maps are maps that assign integer ID values to every cell in the active watershed area. Index maps for distributed parameters are usually based on soil texture, land use, and vegetation classifications. Parameter values are assigned to each cell based on its index number. A table of parameter values is created for each process and assigned an index map.
Index maps
An index map is an array of integer values (one for each grid cell) that represent unique IDs for the different spatially distributed properties being defined. The typical maps (although not restricted to) are derived from:
- A land use (land cover or vegetation cover) coverage.
- A soil texture coverage.
- A combination of land use and soil type coverages where all the combinations of land use and soil texture are determined with an ID created for each unique pair of overlapping polygons.
The Maps dialog is used to create and manage different index maps used in WMS. This dialog is shown in Figure 7.
Several options exist for creating index maps including:
- Importing an existing grid file.
- Mapping a GIS coverage.
- Setting a constant value for all grid cells.
- Interpolating from a data set.
The following sections describe the key elements of the Index Maps dialog.
The Index Maps window contains a list of maps created for the GSSHA project. A new map can be created using the Add Map button, and the Rename Map button can be used to give it a more meaningful name. The Copy Map and Delete Map buttons can also be used to add or delete maps from the list.
The Import button allows a GRASS ASCII grid to be imported and used as an index map. The Import command is primarily used when the GRASS GIS is used as a companion to WMS for GSSHA model development. The imported grid must be of the same resolution as the GSSHA grid already created in WMS. Unless both of these grids are created in GRASS, this is unlikely to be the case. The Export command can be used to save an ASCII grid of the selected index map. This function is most useful if you wish to view the grid with ArcView or other GIS software.
Mapping tables
Mapping tables are used to relate index map IDs to parameter values. The required values depend on which simulation options are selected. The most basic value is surface roughness, but if infiltration, evapotranspiration, or other options are defined then the parameters for each of those options will also need to be defined. The mapping table editor, shown in Figure 7, is accessible by selecting the Mapping Tables… command from the GSSHA menu, or by using the Edit Mapping Tables… button in the index map dialog.
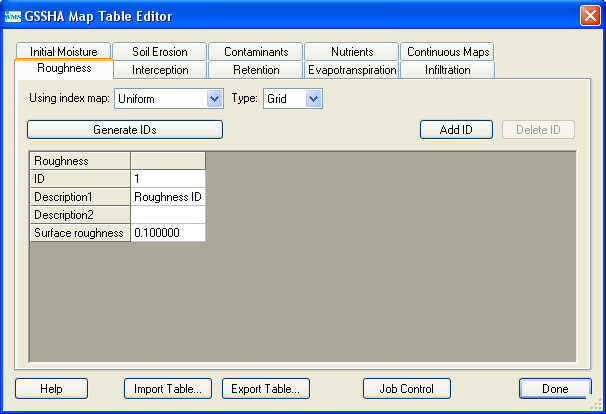
The GSSHA™ Map Table Editor, shown in Figure 8, allows you to select a process, generate table IDs for that process, and define the parameter values for the IDs of the table. If you try to select a process (evapotranspiration, for example) that has not been enabled in the Job Control dialog, you will be prompted to turn on that option if you wish to define parameter values for the IDs. Each active process must be associated with an index map, assigned from the Assigned index map drop-down combo box.
The Generate IDs from map button will generate a new table ID from each unique ID in the map. You can also Add or Delete a given ID using the appropriate buttons. To define parameter values for a given ID, you should select that ID from the ID window. Edit the corresponding values for that process by selecting the appropriate line in the Selected ID Property window and change the value in the edit field just below it.
You can export a table for later use if you have a certain set of parameter values that correspond to a standard classification system of soils or land use. This table can then be imported for use in the development of other GSSHA models.
Assigning uniform parameters
Uniform values are assigned from the Index Maps command in the GSSHA menu. Using this dialog, a new index map can be created, and then the Constant to Array button used to assign a single ID number to every cell in the active grid. This uniform index map may then be assigned to any given process. The uniform index map could be assigned for overland roughness in the following manner. Select the Edit Mapping table button. Select Roughness from the process list and the uniform index map from Assigned index map. ID numbers may be automatically generated from the index map by selecting the Generate IDs from map button. Alternatively, hitting the Add ID button will also generate IDs, but in a numerically sequential order. Parameter values for each ID are entered by selecting the ID number under ID and then filling in the information in the Selected ID property table, which will be Surface roughness in this example. Select Done when finished.
Assigning spatially distributed parameters
One of the greatest assets of distributed hydrologic models like GSSHA is the ability to spatially distribute the parameters for processes, such as overland flow and infiltration, over the watershed. Assigning values, grid cell by grid cell, is tedious and makes all but the simplest and smallest models impossible. Using WMS, GIS coverages (layers) representing land use and soil texture can be used to assign model parameter values to groups of grid cells sharing the same characteristics.
The basic process of assigning spatially distributed parameters consists of the following steps:
- Import a GIS coverage for land use, soil texture, or vegetation type (generally this should be in the ArcView shapefile format).
- Map the land use, soil texture, or vegetation ID to the grid cells using a spatial overlay operation.
- Define parameter values (e.g., surface roughness, hydraulic conductivity, etc.) for the unique ID numbers.
A given soil texture/land use (STLU) index map can be used to assign multiple parameters. Since most of the grid cell parameters can be referenced to either land use or soil properties, a given simulation generally requires only a single index map of each. A combination land use and soil texture index map makes it possible to relate a parameter value to the combination of land use and soil texture (for example infiltration or erosion). Once the index maps are defined, parameter values are assigned to the IDs of the index maps via mapping tables. The combination of the index maps, with ID numbers, and the mapping tables, with the parameter values, are used by GSSHA to internally assign parameter values to each grid cell.
Locating GIS data
The ability to locate and obtain relevant land use and soil texture data is an important part of assigning parameter values to a GSSHA simulation. The World Wide Web is an excellent resource for obtaining data and the WMS developers have created a web site summarizing the key nation-wide (US) data available for download. This web site, maintained at http://www.emrl.byu.edu/gsda, is updated on a periodic basis. It should be noted that the gsda web site references data sources that are maintained and distributed on a nation-wide basis. More accurate (higher resolution and more recent) data are often available from local government agencies and universities, so it is wise to check for alternative data sources.
Elevation data should be requested in either USGS Format or Arc/Info ASCII grid, as described in Chapter 2. Vector coverages representing land use and soil texture should be requested in ArcView shapefile format.
Consistent Coordinate Systems
In order to accurately overlay your land use and soil data with the grid, all of these data must be in the same coordinate system. The data coordinate system depends on the standard of the agency that disseminates data. Some data are in geographic coordinates (latitude-longitude), some in UTM, and a few others in different coordinate systems. Areas and distances cannot be computed directly from geographic coordinates. Although any planimetric (X,Y) coordinate system can be used, it is recommended that you convert all data to the UTM coordinate system. Converting coordinates can be done using ArcView or other GIS software, or using WMS. If using WMS first complete the WMS tutorial to learn how to convert data to different coordinate systems. Information about coordinate systems is also available in the on-line WMS help.
Elevation
Elevation data are essential for delineating the watershed and establishing the initial elevations in the finite difference grid. The gsda web site contains many excellent sources of elevation data throughout the United States and related territories. The WMS reference manual contains more detailed information on importing, displaying, and manipulating DEM data. Chapter 2 of this primer discusses the use of a DEM to delineate a watershed and establish the numerical grid.
Land use
The USGS provides land use classifications for the entire United States at 1:250,000 scale. These data are available from the USGS directly, but in a format called GIRAS, not directly readable by WMS. Arc/Info is required to convert the GIRAS data to a form useable by WMS. The Environmental Protection Agency (EPA), as part of the BASINS program, has converted the GIRAS files to ArcView shapefiles. These data can be downloaded from the EPA, as directed on the gsda web site, and used directly in WMS. A list of land use code descriptions can be read from the Appendix at the following USGS site:
http://edc2.usgs.gov/glcc/globdoc2_0.php
A link to this location can also be found in the gsda web site.
Handling large land use maps
The land use maps downloaded from the EPA site are organized by the USGS 1:250,000 maps. These maps are generally large relative to the size of the watershed being modeled and can tax WMS’s memory resources. There are now two methods for dealing with this problem.
In WMS
First, WMS can now use ESRI's ArcObjects to natively read the shapefiles. The region of interest can then be selected and WMS will then convert only the selected data to the WMS internal format. For more information on this method, please refer to the WMS Help File.
Via ArcView
For the second method of dealing with large data sets, it is suggested that you use ArcView or other GIS software to clip out the region of interest. For example: after delineating the basin as described in Chapter 2, export the basin boundary polygon as a shape file. You can then use the GeoProcessing extension within ArcView to clip out the land use that covers the area of interest. You can also simply make a bounding box that is bigger than the watershed and use it to clip out the desired data. The following lists some details for using ArcView to do this.
- Follow the links on the EMRL gsda website to the EPA basins data and download the required data for your watershed. These data will include both the USGS Land Use/Land Cover data on the 1:250,000 map scale and the Natural Resources Conservation Service (NRCS) STATSGO soil data clipped by watershed Hydrologic Unit Classification (HUC).
- From your delineated watershed in WMS, export the basin boundary as a shapefile.
- Load the basin boundary shapefile into ArcView.
- Load the land use data downloaded for your watershed (often there are multiple 1:250,000 map sheets for a given HUC) into ArcView.
- The land use data are in geographic (lat/lon) coordinates, while your boundary is likely in Universal Transverse Mercator (UTM) or some other planimetric coordinate system. You will need to “project” one or the other data sets so that they are consistent. The following is recommended.
- ArcView contains tools for projecting shapefiles. Versions 8 and 9 have a projection wizard, but there is also a simple tool in the sample extensions called the “projector.” This extension will add a little button to your macros.
- Using the ArcView projection tools, change the land use data from geographic coordinates to the coordinate system of your watershed.
- If your watershed overlaps multiple land use maps, you will need to project all of them.
- While it is possible to use the WMS coordinate conversion (projection) tools, this method requires two conversions. First, the boundary must be converted to geographic coordinates before exporting. The land use and soil data must also be converted from geographic to your working coordinate system after importing. In ArcView only one conversion is required.
- Make sure the geoprocessing wizard extension is on in ArcView.
- Using the Clip command in the geoprocessing wizard, clip the land use data using the watershed boundary polygon.
- If you have multiple land use maps, you will need to clip both and then merge the results (or merge the maps before clipping).
- The clipped land use file can now be imported to WMS as a Land Use type coverage where the LU_CODE attribute is mapped as the WMS Land Use data.
- Make an index table with matching attributes for the GSSHA model based on the LU_CODE parameters. The EMRL gsda website includes a link to the USGS land use information describing the different land use codes. That index table is reproduced here:
Classification codes
- 1 Urban or Built-Up Land
- 11 Residential
- 12 Commercial Services
- 13 Industrial
- 14 Transportation, Communications
- 15 Industrial and Commercial
- 16 Mixed Urban or Built-Up Land
- 17 Other Urban or Built-Up Land
- 2 Agricultural Land
- 21 Cropland and Pasture
- 22 Orchards, Groves, Vineyards, Nurseries
- 23 Confined Feeding Operations
- 24 Other Agricultural Land
- 3 Rangeland
- 31 Herbaceous Rangeland
- 32 Shrub and Brush Rangeland
- 33 Mixed Rangeland
- 4 Forest Land
- 41 Deciduous Forest Land
- 42 Evergreen Forest Land
- 43 Mixed Forest Land
- 5 Water
- 51 Streams and Canals
- 52 Lakes
- 53 Reservoirs
- 54 Bays and Estuaries
- 6 Wetland
- 61 Forested Wetlands
- 62 Nonforested Wetlands
- 7 Barren Land
- 71 Dry Salt Flats
- 72 Beaches
- 73 Sandy Areas other than Beaches
- 74 Bare Exposed Rock
- 75 Strip Mines, Quarries, and Gravel Pits
- 76 Transitional Areas
- 77 Mixed Barren Land
- 8 Tundra
- 81 Shrub and Brush Tundra
- 82 Herbaceous Tundra
- 83 Bare Ground
- 84 Wet Tundra
- 85 Mixed Tundra
- 9 Perennial Snow and Ice
- 91 Perennial Snowfields
- 92 Glaciers
Soils
The Natural Resources Conservation Service (NRCS), formerly the Soil Conservation Service (SCS), has created a comprehensive set of soil coverages. These can be found at three different scales. From least detailed to most detailed they are:
- NATSGO - nation
- STATSGO - state
- SSURGO - county
The STATSGO data have been compiled in ArcView shapefile format by watershed units (large basins) for distribution as part of the EPA BASINS program. Detailed information for downloading STATSGO data is provided on the gsda web site.
The NRCS also distributes the files on a state-by-state basis. The state files are very large. For many states the files are too big to read into WMS without clipping, as suggested in the Land Use section above. A secondary table containing various soil classification information must be joined to the polygons using ArcView prior to using in WMS. The name of this table is “comp.dbf” and should be joined with the polygons based on the MUID field name (present in both the feature attribute table of the polygons and the “comp.dbf” file).
The necessary details for using ArcView to process the soils data follows:
- From your delineated watershed in WMS, export the basin boundary as a shapefile.
- Load the basin boundary shapefile into ArcView.
- Load the soils data downloaded for your watershed into ArcView.
- The soils data are in geographic (lat/lon) coordinates, while your boundary is likely in UTM or some other planimetric coordinate system. You will need to “project” one or the other data sets so that the two types of data are in consistent coordinates. Follow the instructions above in the land use section to do this for the soils as well.
- You must now link the attribute table for soils to the features.
- Open the table “statsgoc.dbf” (included with the Basins data).
- Select the MUID field from this table.
- Open the feature attribute table for your soils.
- Select the MUID field and choose the Join command (this will append the attributes in “statsgoc.dbf” to the soils feature attributes).
- Do this before clipping so that the clipped soils file will contain all of the attributes describing the soils.
- Make sure the geoprocessing wizard extension is on in ArcView.
- Using the Clip command in the geoprocessing wizard, clip the soils data using the watershed boundary polygon.
- Unlike the land use data, there is not a single Soils Code. You now need to “reclassify” based on a soil attribute. The best attribute for “linking” soil properties is probably the Surftex value. This will have values like SIL (silt) LSIL (loamy silt), etc.
- Create a new field for soil attributes that is of type number and name it something like SOILID.
- Examine the set of different soil values and then for each one do the following:
- Run a query to select all soil polygons of the given type.
- Select the new field (SOILID).
- Use the calculator to set an integer ID value (you can go 1, 2, 3, or 10, 20, 30, etc.)
- Save your table with edits.
- Import this clipped, reclassified soil table into WMS. Make sure to import the soil as a NEW coverage that is of type Soil Type.
- Manually map the new field (SOILID) to be the SCS Soil attribute in WMS.
- Make an Index map based on your soil types with the appropriate GSSHA parameters.
Always check for the availability of SSURGO data from local NRCS offices or other local agencies that disseminate GIS data. These data are often available near regions of higher population and land development and provide greater resolution of soil texture data.
Accessing the texture information
The infiltration parameters for GSSHA are derived from Rawls and Brakensiek’s table in which the parameters are listed based on the textural classification of soil. This puts forward the importance of obtaining soil texture information from the soil data. SSURGO soil database has the texture classification information in one of its database files. This information cannot be read in directly into WMS but a tool has been developed using Microsoft Excel which helps to extract the textural classification and few other related information which is useful in GSSHA modeling.
Using texture to create an index map
WMS has an interface to create a soil index map based on soil textural classes. Once this index map is created WMS automatically reads in the values of infiltration parameters from Rawls and Brakensiek’s table which is hard-wired in WMS. These values are basically used for initial basic model set up and need to be refined during the process of calibration.
Assigning spatially distributed infiltration parameters based on soils
The infiltration parameters are stored in .cmt file which can be modified based on the best engineering judgment of the modeler to meet the site condition. The .cmt file has a list of roughness and infiltration parameters which are uniquely identified by the soil textures. Once the soil index map with texture is developed, reading in this .cmt file will populate the parameters into the mapping table.
Adjusting infiltration values based on land cover
The parameters read in through the .cmt files need to be modified as the values of infiltration parameters listed on Rawls and Brakensiek’s table are for bare earth. But most of the times the land surface is covered with some sort of land use and thus the infiltration values need to be modified based on the land cover. For instance, the infiltration parameters for sandy loam in an agricultural field will be different from the sandy loam under some built up area. The parameters need to be modified based on the surface characteristics of the land covering the soil texture.
Another situation when the infiltration parameters need to be modified is during calibration. To match the simulated results with the observed records, calibration needs to be done. During calibration the infiltration parameters need to be modified.
Mapping to the Grid
GIS coverages are used to assign spatially varying grid parameters by mapping the points, arcs, and polygons of a GIS coverage to an index map of unique land use, soil texture, or land use/soil texture IDs. A series of mapping tables that relate the parameter values of the IDs can then be developed. Assigning the GIS coverage IDs to the grid cells is accomplished by selecting the GIS coverage you wish to generate the index map from and then choosing the GIS data -> Selected Index button. Figures 9 and 10 illustrate how the IDs from a land use (or soil texture) coverage are mapped to the finite difference grid.
Once an index map has been created, the individual parameters are assigned for each ID (five in the example shown in Figures 6 and 7) through a mapping table, as described above.
Lake and Channel Routing
A strength of the GSSHA model is the capability to couple surface runoff with channel hydraulics. A new feature added in GSSHA 2.0 is the ability to simulate simple lake storage and routing. Channel flow is simulated as a 1-D finite volume system of links and nodes. Lakes act as storage mechanisms that are able to grow and shrink, changing the water surface elevation in response to inflows and outflows. Both the channel networks and lakes are defined in WMS using feature arcs to create the channel links or outline the lake area. WMS automatically maps the vector streams to the grid cells in order to prepare the input necessary for GSSHA to simulate the interaction between overland and channel flow. Each segment of the channel network must be assigned cross-sectional parameters, and hydraulic structures, lakes, and detention basins may be placed at any point in the network.
WMS has several tools for creating, assigning attributes, and numbering the lakes, links, and nodes. How these tools can be used to easily create the necessary data for channel routing and lake storage is the focus of this chapter. The next section discusses the “nuts and bolts” of the input parameters required by GSSHA. This is followed by a detailed discussion on how to build the proper channel files using WMS.
Besides the identification of grid cells containing the stream channels and the definition of their cross-sectional parameters, several physical constants and simulation parameters for the channel routing and lake storage algorithms must be defined. All of these parameters are defined in the GSSHA Job Control dialog of WMS as discussed in Chapter 3.
Channel routing is defined by either selecting the Diffusive Wave or MESH routing method. If no channel routing is defined, only surface runoff calculations are performed. If the Diffusive Wave method is defined, then the following parameters must also be set:
- Node length - the distance between computational stream channel nodes. This value must be uniform throughout the channel network. The actual node lengths are set by redistributing the verticies along all of the stream arcs and may vary slightly from arc to arc. The minimum permissible node length will vary depending on the velocity of the water in the channels, but a good rule of thumb would be to make them no shorter than 1/2 the cell size.
- Routing time-step - the computational time-step in seconds. At present this value must be equal to the time-step used for overland flow routing.
Links and nodes
Channel flow is simulated as a 1-D finite volume system of links and nodes. Four types of links are available to represent different stream and flow structure. These are channel links, lake and detention basin links, and in-stream flow structure links. Each of these will be discussed in turn.
Channel Links
Channels in GSSHA are represented as linear series of nodes that form links, which in turn can be connected in a network fashion. A node is the basic computational element in channel routing and represents a volumetric portion of a channel. The possible channel link types are presented in Table 2. Currently WMS does not support a fluvial link with dual side slope trapezoidal cross section.
| Description | Num. Parameters per cross section |
|---|---|
| Fluvial link, trapezoidal cross section | 5 |
| Fluvial link, trapezoidal cross section, subsurface parameters | 7 |
| Fluvial link, dual side slopes trapezoidal cross section | 6 |
| Look-up table (break point) cross sections | 2 |
| Look-up table (break point) cross sections, subsurface parameters | 4 |
Table 2. Different channel link types that can be used in GSSHA. WMS supports all but the fluvial, dual-sided trapezoidal cross section link.
Information on the links and nodes is contained in two text files: the channel input file and the grid stream file. The channel input file conveys the cross-section and hydraulic properties of the channels to GSSHA, while the grid stream file is used to relate the position of channel links and nodes to overland flow and saturated groundwater cells. WMS creates these two files from the information entered as the feature arc attributes. Some general features of the channel networks are:
- Looped reaches cannot be simulated.
- Link types cannot be mixed within a link.
Lake Links and Detention Basin Links
Lakes and detention basins are defined similarly in GSSHA. They are represented as a set of cells that are ordered according to elevation. Both the lakes and detention basins must have an outlet structure and a set of embankment arcs that detain the water in the natural relief next to the outlet structure. Lakes and detention basins are stored as part of the channel input file. Three parameters must be specified for each lake or detention basin - the minimum, initial, and maximum water surfaces; lakes and detention basins must have an outlet structure. A lake outlet may be the simulation outlet as well.
Structure Links
Structures links are represented as sets of in-stream locations that reference both upstream and downstream water surface elevations in order to compute flow across or through the defined structure. Structure links are stored in the channel input file. The rating curve and rule curve types allow an implicit representation of the flow mechanics of any structure not explicitly defined. Multiple structures may exist at a single location. The possible structure links are presented in the following table.
| Description | Num. Parameters per structure |
|---|---|
| Weir, horizontal broad crested | 4 |
| Weir, infinite sag vertical curve | 5 |
| Culvert, Round | 8 |
| Culvert, Oval | 9 |
| Culvert, Rectangular | 9 |
| Rating Curve | <curve data> |
| Rule Curve | <curve data> |
| Scheduled Discharge | <curve data> |
Defining stream networks with feature objects
Feature polygons, feature arcs, and feature nodes are used in WMS to create the stream network. These feature objects may be created in WMS or imported from another program. Stream channels are defined by feature arcs, lakes by feature polygons, and detention basins and structures by feature nodes.
Stream Channels
Stream channels are defined in WMS by creating or importing stream feature arcs. These feature arcs have attributes that describe the various hydraulic factors of the channels. Stream feature arcs can be defined using any combination of the tools and import options available in WMS, but typically they will be defined from the results of the stream runoff characteristics computed by TOPAZ and generated during the initial delineation of the watershed from the digital elevations. When using the arcs computed by TOPAZ, make sure that the stream network created does not violate the following rules:
- Stream arcs cannot pass along the edges of cells. They must be moved to one side or the other. Otherwise, WMS is likely to incorrectly define the cells that underlie the channel.
- Stream arcs should not exit the active grid except at the outlet. The arc that exits the grid to form the outlet should terminate shortly after exiting the grid. It is permissible to have the outlet just inside the grid, up to one-half grid cell.
Often, shape files showing the stream location are available. These can be imported into WMS and converted to feature objects or displayed in the background and used as a template for manually constructing the stream arcs. When manually creating stream arcs, all feature lines should be constructed from downstream to upstream.
Lakes
Lakes are represented in WMS as polygons. Lake polygons can either be imported from GIS files or created manually in WMS. Lake polygons serve as reference features and are not actually used by GSSHA. In GSSHA lakes are sets of cells that have been ordered from lowest elevation to highest elevation. This elevation ordering allows GSSHA to fill and drain the lake as it would naturally occur. As the lake is allowed to shrink to, but not below, the minimum water surface elevation, care needs to be taken that channel links entering the lake polygon extend to the minimum water surface elevation cells. The minimum, initial, and maximum water surface elevation cells can be displayed by turning on the appropriate options in the 2D grid display options dialog. The following figure shows how the channels need to extend to the minimum water surface elevation.

Another important aspect of modeling lakes is their delineation. Lakes in GSSHA are represented as a set of cells, ordered by elevation, which describe how the lake should fill and drain. The extents of the lake cells are determined by the interplay of four variables:
- the minimum, initial, and maximum water surface elevations
- natural topography and bathymetry
- the location of the lake outlet
- the location of embankment arcs.
The minimum and maximum water surface elevations control the growth and shrinkage of the lake while the initial water surface elevation controls the initial lake level. These values are set in the polygon attributes dialog. Good topography and bathymetry are very important for the cells between the minimum and maximum water surface elevations. The location of the outlet and the embankment arcs is critical to the successful delineation of the lake. All lakes must have both an outlet structure and embankment arcs restricting the growth of the lake. The only exception to this rule is for a lake that is only restricted by the grid boundaries because the lake outlet is also the simulation outlet.
Outlet and embankment arc placement is critical for successful lake delineation. The lake delineation is done automatically by WMS but controlled by the placement of the lake outlet and associated embankment arcs. Embankment arcs are not mapped directly to GSSHA as input but are interpolated to cell boundaries where they become embankment edges and impede flow from one cell to another. In placing the lake outlet and embankment arcs, care should be taken to make sure that the outlet is upstream of the embankment edge, even though the arc should be attached to the lake outlet. The delineation routine for the lakes begins at the cell containing the lake outlet and searches nearby cells, adding them to the lake cell list, until it runs into a) a cell above the maximum water surface elevation, b) the grid boundary, or c) an embankment edge. If the embankment arcs are incorrectly defined (e.g. do not reach cells above the maximum water surface) it is quite possible for the lake delineation routine to continue downstream and incorrectly engulf major portions of the simulation. This is not to say that flow cannot overtop the embankments, only that embankment arcs should be placed so as to correctly allow the lake to be delineated. Embankment arcs are covered in-depth in the next chapter, including how to define low spot locations where water may overtop the embankment. The following diagram shows an example of the correct placement of embankment arcs and the lake outlet.

Structures and Detention Basins
Hydraulic structures and detention basins are represented in WMS as feature points. Several hydraulic structures may be defined at a single location. For example, a double box culvert where a road intersects a small stream may be represented as two square culverts and a broad-crested weir representing the road in case of overtopping. Detention basins are treated as lakes and must also have an outlet structure at the same feature point that represents the detention basin. The above rules about embankment arcs and lake outlets also apply to detention basins.
Link types
Once the feature points, arcs, and polygons are defined, the link types and their associated parameters are assigned to the feature arcs, nodes, and polygons. Fluvial streams are represented as feature arcs, hydraulic structures as feature points, lakes and ponds as feature polygons, and detention basins as feature points.
Fluvial streams
Two general types of streams can be created, Trapezoidal and Irregular Cross-section, as shown in the Feature Arc Attributes dialog in the following figure. WMS now automatically assigns internal GSSHA link numbers to all of the link types.
Nodes at the junction of stream sections are known as Link Breaks. Link Breaks desired at other locations must be assigned manually by selecting a feature vertex and converting the vertex to a node using the Vertex <-> Node command in the Feature Objects menu. If there is no vertex at the desired location, then you must create one. Arcs can be assigned as streams by selecting the arc and then defining it as a stream under the Attributes menu.
Cross sections for both the trapezoidal and irregular streams are defined by selecting feature arcs using the select feature arc tool while in the Feature Line Module. While in the Map Module, and with the link or links selected, select Attributes under the Feature Object menu. Trapezoidal and break point cross sections can then be defined in Feature Arc Type dialog box.
Trapezoidal cross sections
Trapezoidal cross sections are defined by:
- Bottom width (m).
- Channel depth (m).
- Side slope (change in X with a change in Y of 1).
- Manning’s N - Manning’s roughness coefficient, n (dimensionless).
Irregular cross sections
Look-up tables or break point cross sections are used when actual field surveyed cross-sectional data are available. After selecting Break point cross section arc, click on Define Cross section parameters. From here you can import, create, or edit values in the look up table, and then assign look up tables to stream sections.
The parameters in the look-up table are:
Depth (m) Area (m2) Top width (m) Conveyance (AR2/3/n)
These values may be entered directly into the table, imported from a separate program, or computed from the cross section. To create a new table, select New; a dialog box will appear asking for the number of increments in the table. The default value is 8. Any number of segments in the table can be specified. The number of segments should be commensurate with the size of the cross section. Too large a change in the look up table values may cause GSSHA to crash. If in doubt, increase the number of values in the table.
To construct a table from measured points from the cross section, select Compute Parameters from Cross section… at the bottom of the dialog box. Another dialog box appears asking for the type of units to use, English or Metric, and the value for Manning’s n. This value is used to compute the conveyance. The default value is 0.01. After selecting a unit system and assigning a Manning’s n, an X,Y series editor appears. Surveyed points are entered with this editor. Surveyed X,Y points may be imported using the Import button on the right-hand side of the editor, or values may be entered manually for each point under X and Y at the left-hand side of the screen. Values of X must increase with successive points. Values of X and Y may be positive or negative. As values are typed into the editor, points appear on the screen to the right. The location of these points may be adjusted by selecting the Select Data Point tool (three dots with an arrow in the center) and then clicking and dragging the point to the desired location. Additional points may be added by selecting the Add Data Points tool (the three dots below the Select Data Point tool) and clicking on a point inside the X,Y Screen. Additional cross sections may be created by clicking on New and defining the points as described above. You will want to provide a meaningful name for each channel cross section and corresponding table. Once all the points are entered select OK, and the Table Parameters will automatically be computed.
Once all the tables are created, tables can be assigned to a link by selecting the link, selecting Attributes under Feature Objects, toggling on Break point cross section arc, selecting Define Cross section Parameters, and then selecting the name of the table from the list that appears on the left-hand side of the dialog box.
Smooth transitions in channel cross-sectional properties between all connecting fluvial links often play a vital role in the success of simulations. Abrupt changes in cross sections can lead to numerical mass conservation errors. It may be necessary to create transition links between measured break point and trapezoidal cross sections when adjoining links vary greatly in cross section. It may also be necessary to assign different channel cross sections within a link. In WMS this can be done by breaking a single link in to two or more links and assigning different cross sections to each of these links. Sometimes it is necessary to provide a different cross section for every node in a link or along the entire channel. To do this, the channel input file will have to be manually edited. Users should consult the GSSHA User’s Manual for more information on the format of the channel input file.
Hydraulic structures
Internal boundary conditions, such as weirs and culverts, are defined at nodes along the feature arc network. Internal boundaries are given a unique link number and parameters are defined for these nodes in the same way as they are defined for the feature arcs. These internal boundary conditions represent point features of the channel network. To add an internal boundary condition, select the feature point at the proper location. You may need to add a new feature node or convert a feature vertex to a feature node by selecting the feature vertex, and then selecting vertex<->node under the Feature Objects menu. There are eight hydraulic structures possible; five explicitly defined and three implicitly defined. The parameters needed for each of the hydraulic structures are given below.
Horizontal Broad Crested Weir
- Crest length
- Forward flow discharge coefficient
- Reverse flow discharge coefficient
- Crest low point elevation
Infinite Sage Vertical Curve Weir
- Left slope
- Right slope
- Forward flow discharge coefficient
- Reverse flow discharge coefficient
- Crest low point elevation
Round Culvert
- Diameter
- Upstream invert elevation
- Downstream invert elevation
- Forward flow inlet loss coefficient
- Reverse flow inlet loss coefficient
- Slope
- Length
- Manning’s roughness
Oval Culvert
- Axis width
- Axis height
- Upstream invert elevation
- Downstream invert elevation
- Forward flow inlet loss coefficient
- Reverse flow inlet loss coefficient
- Slope
- Length
- Manning’s roughness
Rectangular Culvert
- Box width
- Box height
- Upstream invert elevation
- Downstream invert elevation
- Forward flow inlet loss coefficient
- Reverse flow inlet loss coefficient
- Slope
- Length
- Manning’s roughness
Curve Types
There are three curve types available for implicit representation of hydraulic structures. These are a rating curve, a rule curve, and a scheduled discharge. A rating curve is a piece-wise linear set of stage-discharge values. A rule curve is a step-wise linear set of stage-discharge curves. The scheduled discharge curve is a set of time-discharge values.
Lakes and Detention Basins
Lakes and detention basins are defined spatially by the location of the feature point representing the outlet of the lake or detention basin. There are three parameters used by WMS and GSSHA to define the extents of the lake. These parameters are accessible from the lake polygon attributes for lakes or the feature point attributes for the detention basins. These three parameters are the minimum water surface elevation, initial water surface elevation, and the maximum water surface elevation. The initial water surface elevation is the water surface at the beginning of the simulation. The minimum and maximum water surface elevations represent simulation limits. The minimum water surface elevation is imposed so that no stream channels need to be artificially created through the lake bottom; the maximum water surface elevation represents a guess at the greatest extent of the lake in order to limit lake growth to a contiguous area.
Node spacing
Correct node spacing is important for successful simulations. The stream routing algorithms use a finite volume solution. In the volumetric equations both the channel shape and the channel length are important factors. GSSHA uses a constant node spacing in order to help mitigate numerical instability problems from having too large or too small of nodes next to each other. Since GSSHA is expecting a constant node length then the stream network must be set up to have a constant node length. The node length is the length between verticies on the stream arcs. Small differences in stream node length are acceptable but not desirable. If the actual node length is very different from the specified node length the calculated depth of water in the channel will be off and thus throw off the hydraulic gradient which drives the flow. The flow in the channel could be significantly altered from what it should be if the actual node spacing is very different from the specified node spacing.
The actual node lengths are set by redistributing the vertices along all of the stream arcs. Node lengths may vary slightly from arc to arc. The minimum permissible node length will vary depending on the velocity of the water in the channels, but a good rule of thumb would be to make them no shorter than 1/2 the cell size. In WMS the redistribute vertices option is available in the Feature Objects | Redistribute... menu command or the Smooth GSSHA Streams dialog.
Smoothing the profile
The channel input file contains the channel bed elevation at each node, which constructs the longitudinal profile of the deepest portion of each channel (thalweg) in the drainage network.
Ideally, you will use surveyed cross sections and thalweg profiles of the channel network. However, extensive surveys are often impossible for the entire drainage networks of large watersheds. In lieu of an extensive survey, there are existing tools for extracting channel topology from digital elevation data. If the channel network is extracted from the digital terrain data, smoothing of the channel thalweg must be performed to produce physically realistic longitudinal profiles because of errors inherent in any digital data. The algorithm developed by Ogden (Ogden, Saghafian, and Krajewski 1994) has been embedded in WMS so that the streambed elevations along the channel network can be smoothed. The following guidelines should be followed when smoothing channels:
- First, redistribute the entire stream network to have a vertex spacing somewhere close to the cell size, plus or minus 1/2 cell size. It is important that the vertex spacing be consistent and fairly similar to the cell spacing. This step also simplifies the streambed smoothing process.
- Streambed elevations should always be lower than adjacent surface elevations. WMS recognizes both the streambed elevation at each vertex and a surface elevation at each grid cell. When smoothing of channels is done, only the streambed elevation is changed.
- Abrupt transitions in streambed elevation should be avoided. If abrupt transitions occur naturally in the stream (e.g., a headcut), a weir can be inserted to simulate this feature.
- Topographical maps of the watershed can be very useful in detecting obvious errors in the DEM that cause unusual features in the stream profile. Unusual profile features extracted from the DEM can usually be removed without significant effects on the simulation results.
To redistribute the vertex spacing of the stream network, use the select network tool in the Map Module, click on the downstream-most stream arc, and then choose Feature Objects->Redistribute. Smoothing of the streambed profile and inputting or adjusting the streambed elevation of individual nodes is done under the GSSHA menu, while in the Map Module. First, select the stream segment you wish to smooth using the Select Feature Arc tool. Hold down the shift key to select multiple segments; select from downstream to upstream. You cannot select multiple branches along a stream. Next, under the GSSHA menu, select Smooth Stream Cells. The Streambed Elevation Smoothing dialog will appear, showing the stream bottom elevation in blue and the ground elevation in red (Figure 12). If the stream has not already been edited, the two lines may fall on top of each other and appear as one blue line. There are several options for adjusting the streambed profile. Clicking the Interpolate stream elevations button will automatically smooth the channel, but with varied success. The continued clicking of this button results in successive smoothing of the streambed. The Smooth stream elevations to smoothed grid button will force the arc to conform to the interpolated grid surface, which is often smoother then the original DEM but at a lower resolution. This option inserts many vertices into the arc and thus makes manual editing a chore so a warning message is displayed before WMS will continue to edit the profile.
In addition to using the Interpolate stream elevations option, the elevation of individual nodes can be adjusted by selecting the node with the Select Feature Point tool. The selected node can be moved by holding down the mouse button and dragging and dropping the node at the desired elevation. The exact elevation for the node can also be typed in at the bottom of the display in the Stream Elevation edit field. Typically, it is necessary to manually move points into an approximate shape and then use the Interpolate stream elevations feature to smooth out remaining irregularities.
The Offset stream elevations by constant button is used to adjust all the elevations of the streambed up or down by a specified amount. This option could be used effectively if the stream is generally a specified distance below the ground surface. It is important to check for continuity to the stream segments above and below those being edited as this option can cause significant disruptions in the streambed profile.
Troubleshooting channel routing problems
The explicit diffusive wave scheme employed in GSSHA naturally diffuses, or smoothes, the water surface profile between sharp transitions. The scheme also contains a number of internal stability checks and will typically run on a properly prepared channel network. As discussed above, essential to a properly prepared channel network are smooth transitions between channel cross sections and thalweg elevations.
Problems typically arise when cross sections change abruptly, the thalweg elevation changes abruptly, there are regions of adverse slope in the channel section, or the channel thalweg is above the overland cell elevation. These situations should be eliminated from the beginning. If regions of adverse slope (slope is in the general upstream direction) really exist in the channel network, then it may be possible to include them in the channel network.
Once a problem occurs during channel routing, the task of the user then is to identify the location of the problem. When channel instability occurs, usually because of negative depths caused by numerical oscillations, the model ceases execution and prints warning statements identifying the problem nodes. The user should look at the node/link pairs involved and try to identify the problem. The problem can typically be corrected by smoothing the channel thalweg and/or increasing the number of channel cross sections, or reducing the depth increment in look-up tables. If a surveyed longitudinal profile is causing the trouble, it may be necessary to reduce the channel time-step or do some minimal smoothing of the profile.
Tips on creating lakes
- Set up one lake at a time. When it is working, go on to the next lake.
- Make sure outlets are placed upstream of the embankment.
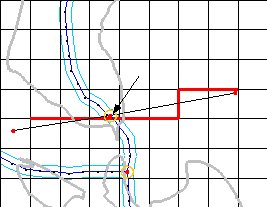 |

|
| Fig. 17. Good | Bad |
- Lakes are filled according to cell elevation. Streams need to be swallowed from downstream to upstream. Thus, the cell elevations along the streams must always increase from the min WSE cells to where the stream enters the max WSE.
 |

|
| Fig. 18. Good | Bad |
 |
|
| Fig. 19. Good | Bad |
- Set the minimum WSE to cover the cell elevation irregularities along any (supposed) stream network in the lake bottom.
- You don’t have to have a stream going through the lake. You can have a polygon a little smaller than the minimum WSE and have the incoming streams connect to it.
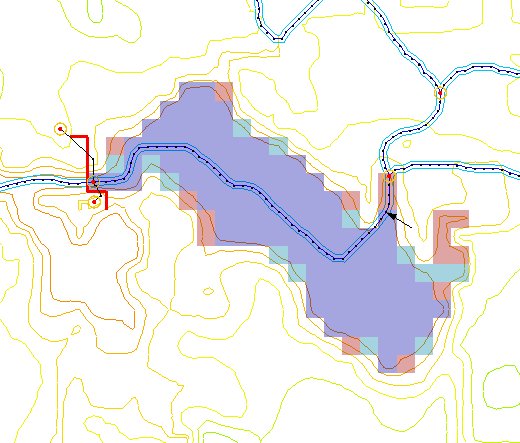
|
| Fig. 20. |
A lake with a stream running through it. The stream will not be used in the simulation from the arrow onward because it is below the minimum water surface elevation. (Note that part of the stream, just below the arrow, that exits the lake. The stream must be realigned to lie within the lake for the lake to work properly.)
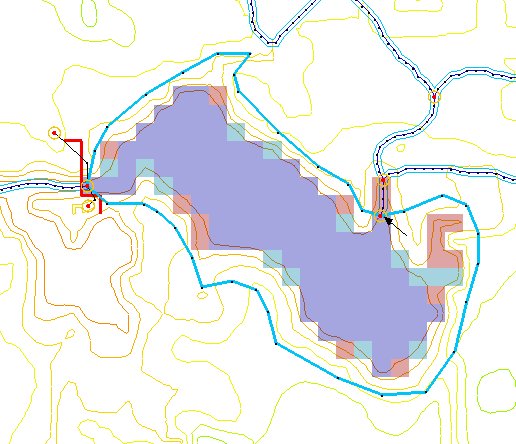
|
| Fig. 21. |
The same lake as above, but defined on a polygon. The extents of the polygon do not actually enter into the calculations of the lake extent in GSSHA; they are merely for visual reference. The lake polygon is only used to assure stream connectivity. One very important point, however, is that the incoming streams need to extend into the minimum water surface elevation zone. As all stream arcs entering and exiting the lake must be connected to the lake polygon, the boundary of the lake polygon must also be inside the minimum water surface elevation at the point where the lake and an incoming stream meet.
- Set the maximum WSE to be the biggest the lake could realistically ever grow. There is no problem if the lake doesn’t grow to the maximum extent during a simulation. There will be problems if during a simulation the lake tries to exceed the maximum water surface elevation.
- Don’t set the maximum WSE so high that adjacent areas of ponding (i.e. what should be neighboring lakes) are included. The lakes grow in order of lowest to highest cell elevations and thus GSSHA cannot realistically simulate a disjointed lake bottom. You can put an embankment there separating the two lakes and actually make two lakes
|
| Fig. 22. |
There are two problem areas here relating to the previous point. The first is in the lower left where a stream cuts across a divide. The lake order thus dictates that disjointed portions of the stream may be flooded. This is not allowed to happen in GSSHA. The other problem is similar in nature in that as the lake rises it is able to capture a stream at a disjointed location.

|
| Fig. 23. |
One way to solve these problems is to create a lake polygon for the lower lake. This eliminates the internal drainage patterns of the lake and simplifies the problem. To solve the disjointed capture of the stream, another lake was created where the ponding after the capture would occur. At the connection point a low spot in the embankment was placed (at the arrow) allowing the two lakes to communicate. An alternative to the one large lake polygon would have been to create a few smaller lakes separated by embankments but with low points allowing the smaller lakes to communicate and act together as a larger lake.
- If there are ponding areas adjacent to lakes (i.e. adjacent ponded cells above the max WSE) you probably ought to have a stream there.
- The cell in which a stream outlet is placed must be below the minimum water surface elevation.
Embankments
Man-made embankments, such as roads or levees, represent an overland flow hydraulic structure that retains, directs, and controls flow. Flow is retained as it is impounded behind the embankment, directed to flow adjacent to the embankment towards natural stream channels, and controlled in a weir-like fashion as it flows over the top of the embankment. Embankments significantly alter the flow characteristics of a watershed and are important features to be able to model.
Embankment arcs in WMS
In WMS, man-made embankments are represented as embankment arcs. These embankment arcs are placed along the centerline of the actual embankment. Often these embankment arcs represent roads that cross a drainage. The embankment arc can intersect a stream arc and an in-stream hydraulic structure (a culvert) placed at the intersection to allow water to pass through. For the embankment arc to function correctly in GSSHA, the elevations along the top of the arc must be defined. This is done through the Embankment Arc Profile Editor.
In the Embankment Arc Profile Editor the arc elevations are generated by entering the parameters for a vertical curve. WMS will then take the given parameters and compute the correct elevation values for each vertex of the arc. The parameters needed for the vertical curve are the elevation of the point of vertical intercept, the left (back) tangent slope, the right (forward) tangent slope, and the curve length. Note that the arc need not be a straight line in plan view for the vertical curve to be computed. Below is an example of an embankment arc profile set by creating a vertical curve.
The Embankment Arc Profile Editor is accessible from the feature arc attributes dialog in the GSSHA coverage. The feature arc type must be set to Embankment Arc before the Edit Embankment Profile button will be undimmed.
Embankment arcs in GSSHA
Often embankment features are smaller (width-wise) than a grid cell and are poorly represented on a coarse or even fine 2D grid of elevations. In WMS, the embankments are represented as feature arcs and are given profile elevations that define the top of the embankment. These feature arcs are then mapped to the nearest cell edge. The embankment acts all along the edge, interrupting flow between the two adjacent cells.
In GSSHA, the embankments are represented as walls between cells. Once the water elevation in the cell reaches the lowest point of the embankment elevation profile that is in that cell, the embankment begins to act like a broad-crested weir. When the embankment acts as a wall, the water in the cells behind the embankment is stored and/or routed along the embankment to the nearest point of flow by the overland flow code.
Low Points
Low points on the embankment arc should be set to be feature nodes and the low point attribute should be set for them. Once the water elevation has risen to this level then water will commence flowing over the embankment in a horizontal broad-crested weir fashion. A toggle box beneath the feature node type selector in the Feature Point/Node Type dialog sets the low point attribute. The elevation of the low point is set in the corresponding edit field. As an embankment acts as a horizontal broad-crested weir in the event of overtopping, the Cell Edge Length Fraction edit field is to designate a portion of the cell edge width as the weir width and ranges from 0.0 to 1.0. The feature node type may be set to any type desired and does not affect the status of the low point.
The low points of embankment arcs are specified by making a feature vertex into a feature node and then checking the low point toggle box.
Summary
Embankment arc represent overland flow hydraulic structures. As they are usually smaller than the grid cells in width they are represented as a wall/weir combo along the grid cell edge. To create an embankment arc, trace out the feature arcs in WMS along the centerline of the actual embankment and then set the arc type to Embankment Arc. Embankment arcs often represent roads so a vertical curve calculator is available in the Embankment Arc Editor dialog where the elevation profile of the embankment can be adjusted. Finally, the lowest elevation points of the embankment arcs must be identified and the nearest vertex turned into a node with the low point feature turned on and the low point elevation set.
Wetlands
Wetlands are important both hydrologically and ecologically. GSSHA 2.0 includes a new capability to model wetlands. The wetlands model is part conceptual and part physical.
Wetlands conceptual model
Wetlands are unique in their hydrologic characteristics in that they closely couple groundwater flow, surface water flow, and water storage. GSSHA employs a conceptual model that operates on a cell by cell basis.
Overview
The model that GSSHA uses allows infiltration and exfiltration, lateral seepage flow, flow through dense vegetation, and flow overtopping the vegetation.
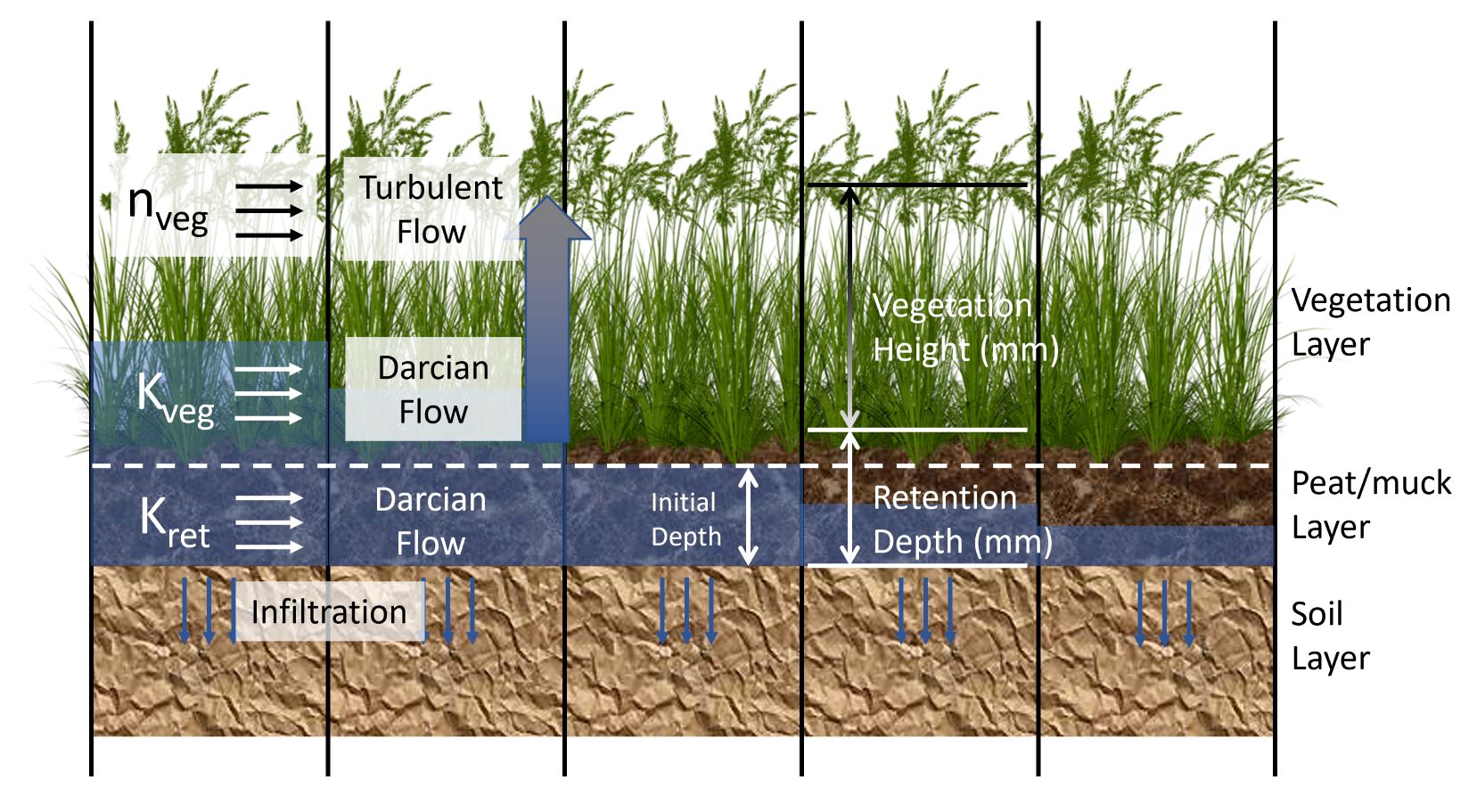
Wetlands setup
Wetlands are specified in GSSHA by including the wetland mapping table in the mapping table file. An index map related to the mapping table can be developed as described below.
Wetlands are set up in WMS through creating a wetlands polygon. This polygon is in the same coverage as the stream data for the GSSHA simulation. When creating the polygon, be careful not to click on or very close to any stream arcs. Once the polygon is created, set its attributes to be a wetlands polygon. The following parameters must be defined and are uniform across the polygon extent.
- Initial Depth (mm) - Initial depth of water in the cell, from the bottom of the retention depth.
- Retention Depth (mm) - Depth of the peat layer. This value is actually subtracted from the elevation grid inside of GSSHA.
- Retention Depth Hydraulic Conductivity (m/day) - Lateral seepage hydraulic conductivity through the peat layer.
- Vegetation Height (mm) - Height of the vegetation above the peat layer.
- Vegetation Height Hydraulic Conductivity (m/day) - Lateral seepage hydraulic conductivity through the bottom of the vegetation.
- Inundated Vegetation Manning's Roughness - Manning's roughness value after the vegetation is overtopped (and possibly flattened.)
To visualize the wetland cells that underlie the polygon, turn on the wetland cells option in the 2D Grid Display Options dialog. WMS creates a new wetland mask map consisting of zeros, no wetland, and integer numbers specified from the wetland polygons. Wetland routing occurs whenever GSSHA encounters a specified wetland cell and using the wetland parameters, as specified above, related to the cell wetland mask number.
Spatially and Temporally Varying Rainfall
The ability to assign uniform rainfall over the entire watershed is maintained largely as a trouble-shooting feature and is mostly used in initial model development. Real watersheds are modeled with temporally and spatially varying rainfall. As briefly described in Chapter 3, all precipitation inputs are created in WMS by selecting Precipitation from the GSSHA Menu while in the 2-D Grid module. This will bring up the GSSHA Precipitation dialog box. How to assign temporally varying rainfall for one or more gages is described below.
Temporally varying, spatially uniform rainfall
Temporally varying, spatially uniform rainfall can be assigned by toggling on the Single Gage Rainfall button. A single-gage rainfall produces a time series of rainfall for the entire watershed. The time series is specified by clicking Define Event and entering the time series with the X,Y data series editor. A single rain gage event can also be constructed in the same manner as described below, where spatially and temporally varying rainfall simulations are discussed in more detail. For a single temporally varying rain gage, the maximum number of rainfall data points in the time series is limited to 1,500. Larger rainfall events can be modeled by GSSHA but cannot be brought into WMS for manipulation. These rainfall files, as well as multiple rain gage files, can be constructed with an editor outside of WMS, and then this file can be named as the rainfall file when saving the GSSHA project file.
Temporally varying multiple gage rainfall
To assign rainfall data from recorded gages, toggle on Multiple-Gage Rainfall, and select a method of distributing the rainfall, by either Thiessen polygons or Inverse distance weighted. WMS does not currently support the file GSSHA requires for temporally varying multiple rain gage input. If you select View Event File, WMS will automatically put you in an editor to create or edit the necessary file. The default editor is Microsoft Notepad. The file may also be created separately from WMS with any appropriate software.
The rainfall file consists of storm event header information, a description of each rain gage, and then cards with a time and value for each rainfall data point. For long-term simulations with multiple rain events, the single-event format is repeated for each additional event.
At the top of the file is a description of the event. This is followed by the number of rain data points in the rain time series. The next line specifies the number of rain gages. This is followed by a series of four-column lines containing the easting, northing, gage name, and the time series name for each rain gage. Rain gages need not be located within the watershed of study. If a gage falls in a different UTM zone to the left of the zone the watershed is in, then negative values can be entered.
Rain gages located well outside the watershed under analysis generally provide poor rainfall estimates. The instantaneous correlation distance for convective rainfall is typically on the order of a few kilometers. Use caution when using data from rain gages further than a few kilometers from the catchment.
The remaining lines at the bottom of the rain gage file reflect the temporal variation of rainfall intensity. The number of columns per line equals the number of rain gages, each being separated by space. The number of lines in this lower portion is equal to number of rainfall periods (NRPDS).
Each rainfall file must have the following cards:
- EVENT – simple description string of the event, must be set in double quotations.
- NRGAG - number of rainfall gages to follow (integer value).
- NRPDS - number of rainfall data points to follow (integer value).
- COORD - coordinate, easting and northing of gage, one card for each gage (NRGAG), must have an identifying string in double quotations, and need not have the same number or locations of gages for different storm events when multiple events are simulated.
- GAGES, RADAR, RATES, ACCUM - rainfall data point. The number of these cards must be NRPDS. Each card specifier should be followed by Year, Month, Day, Hour, Minute, and then one value of rainfall (decimal format) for each NRGAG. The proper card name depends on the type of rainfall entered. The four types are:
- GAGES - rainfall accumulation (mm) over the last time period.
- RADAR -rainfall rate (mm×hr-1) for the last time interval.
- RATES - rainfall rate (mm×hr-1) for the next time interval.
- ACCUM - cumulative amount of rainfall up until that time period (mm).
- Some guidelines for use are:
- Specified rainfall types cannot change within a storm event.
- The time interval can be any value, but there must be a rainfall value for each NRGAG.
- Separate values with spaces or tabs.
- Names of events and gages are NOT optional and must be in double quotation marks, as shown below.
The proper format is shown below. For this example there are three gages and five rainfall data points. The GSSHA User’s Manual should be consulted for additional information on constructing rainfall files.
Within GSSHA, the values of rainfall at the gages are interpolated to the grid cells. Either Thiessen polygons or inverse distance-squared interpolation are used. For RADAR type rainfall inputs, Thiessen polygons should be selected.
Long-term Simulations
The GSSHA predecessor, CASC2D, was originally developed as an episodic model, and GSSHA can still be used to simulate single events with a specified simulation time. However, Senarath et al. (2000) showed the pitfalls of calibrating distributed parameter models like CASC2D to single events. CASC2D was subsequently modified to be able to simulate multiple rainfall events over an extended period. Typically, GSSHA is run in the long-term simulation mode.
There are no restrictions on the duration of the simulation or the number of rainfall events that can be simulated. Annual simulations have been successfully performed for a variety of watersheds. The only requirement is that hydrometeorological and rainfall data be available for the simulation period.
How GSSHA operates during a long-term simulation depends on the model options selected. When GAR is used to calculate infiltration, GSSHA operates in a dual mode. During rainfall events, GSSHA performs in the normal episodic rainfall/runoff mode. Once a user specified minimum discharge is reached on the recession limb of the hydrograph, the rainfall/runoff model is stopped and soil moisture calculations begin. At this point, GSSHA performs hourly evapotranspiration and soil moisture calculations until another precipitation event begins. If saturated groundwater calculations are chosen, then saturated groundwater and infiltration are calculated on a continual basis. See the GSSHA User’s Manual for more information.
When Richards’ equation is chosen as the infiltration option, Richards’ equation is continually solved so that infiltration, evapotranspiration, soil moisture accounting, and groundwater recharge are calculated whether or not rainfall events are occurring. When a rainfall event does occur, precipitation distribution, interception, retention, overland flow, and channel routing are initiated, assuming these processes have been selected for simulation. These processes continue as long as there is rainfall. After rainfall ceases, overland and channel flow continue until water on the overland flow plane and channels ceases to flow. As the decision is based on process conditions, any process may begin or end at any time. The minimum flow criteria discussed above is still used to describe events, but it is used for accounting purposes only and is not used to stop the execution of any processes.
Global parameters
Global parameters for long-term simulations are defined by selecting Job Control from the GSSHA menu, while in the 2-D Grid module. This produces the GSSHA Job Control Parameter dialog box. Check Long-term Simulation and press the Edit Parameters... button and assign the following values in the Continuous Simulation dialog box.
- Latitude – used in radiation calculations for missing data, decimal format (degrees).
- Longitude – used in radiation calculations for missing data, decimal format (degrees).
- GMT – deviation from Greenwich Mean Time (GMT) (+/- h), e.g.
- Pacific Standard Time is -8.
- Mountain Standard Time is -7.
- Central Standard Time is -6.
- Eastern Standard Time is -5
- Minimum event discharge –discharge on the recession limb to stop event simulations when using GAR and to stop event accounting when using Richards’ equation to calculate infiltration (m3×s-1).
- Soil moisture depth – depth of soil column over which evapotranspiration is distributed (m). For GAR, this is the total depth of the soil column from which ET can occur. For Richards’ equation, this is the maximum depth for distributing potential ET demand. See Chapter 11.
- Hydrometeorological (HMET) Data File - name of hydrometeorological data file.
- HMET Format - format of hydrometeorological data file. Toggle on either.
- Samson.
- Surface Airways.
- WES.
See the following discussion of Hydrometeorological Data.
Infiltration model
When long-term simulations are conducted, the infiltration type, selected in the GSSHA Job Control Parameters dialog box, must be either Infiltration redistribution (GAR) or Richards’ infiltration. The necessary parameters for modeling infiltration with GAR are discussed in Chapter 4. A discussion of Richards’ equation is presented in Chapter 11.
Evapotranspiration model
When performing long-term simulations, a method to model evapotranspiration is also selected in the GSSHA Job Control Parameter dialog box. The two methods available are Deardorff Method and Penman Method. The Deardorff method is a bare-soil evaporation model. The Penman Monteith method calculates the combined effect of evaporation and plant transpiration, and requires additional information on the plant community in each grid cell. When the Penman method is selected, the option to vary the entered values of vegetation canopy resistance according to the season is available. When this option is selected, by toggling on the Seasonal Resist button, midgrowing season values of canopy resistance are entered and are automatically varied throughout the year as described in the GSSHA Users Manual. The canopy resistance varies as shown in Figure 24.
Depending on the method of ET selected, the following distributed parameters are input through the mapping tables as described in Chapter 5. Values may be assigned based on field measurements, or from land use and vegetation information. Literature values based on land use, snow cover, and vegetation characteristics are compiled in the GSSHA User’s Manual.
Deardorff
- Land surface albedo – fraction of radiation reflected back to the atmosphere, range 0.0 to 1.0.
Penman-Monteith
- Land surface albedo - fraction of radiation reflected back to the atmosphere (dimensionless), range 0.0 to 1.0.
- Vegetation height (m).
- Vegetation transmission coefficient – direct solar radiation penetrating the vegetation canopy and reaching the ground, range 0.0 - 1.0.
- Canopy stomatal resistance– resistance of the canopy to transpiration at noon (s/m).
Hydrometeorological data
Hourly values of the following hydrometeorological data must be specified for the long-term simulation period:
- Barometric Pressure (in Hg)
- Relative Humidity (%)
- Total Sky Cover (%)
- Wind Speed (kts)
- Dry Bulb Temperature (oF)
- Direct Radiation (W×h/m2)
- Global Radiation (W×h/m2)
The needed data can be obtained from a variety of sources including the National Climatic Data Center (NCDC) and commercial vendors (such as Earth Info). All seven parameters are contained in data sets referred to as Surface Airways data by most sources. These data are used to perform evapotranspiration calculations.
Because of the variety of data sources, GSSHA will read the data in a variety of formats. These are:
- SAMSON, Surface Airways, and U.S. Army Engineer Research and Development Center/WES. The SAMSON format is developed for the NCDC historical database of Surface Airways data called SAMSON. These data files may be purchased from the NCDC in the form of a CD, which contains all historical data from 1961-1990.
- If more recent data are required, they can also be purchased from the NCDC in the Surface Airways format. These file formats contain numerous data parameters in addition to the seven required inputs above.
- All sources of data can be transferred to the WES format containing only the data required by the model. A sample of the ERDC/WES format is shown below. Examples of the other formats can be found in the GSSHA User’s Manual.
WES formatted data
The HMET_WES format contains the following numbers in columns 1 through 11:
| 1. | Year (4 digit) | ||
| 2. | Month | ||
| 3. | Day | ||
| 4. | Hour | ||
| 5. | Barometric pressure | (inches Hg) | No Data (ND) = 99.999 |
| 6. | Relative humidity | percent | ND=999 |
| 7. | Total sky cover | percent | ND=999 |
| 8. | Wind speed | knots | ND=999 |
| 9. | Dry bulb temperature | degrees F | ND=999 |
| 10. | Direct radiation | Watt hour per meter squared | ND=9999.99 |
| 11. | Global radiation | Watt hour per meter squared | ND=9999.99 |
and appears in the following format.
| 1995 | 4 | 14 | 23 | 29.625 | 86 | 100 | 000 | 53 | 9999.9 | 9999.9 |
| 1995 | 4 | 15 | 0 | 29.625 | 83 | 100 | 003 | 53 | 9999.9 | 9999.9 |
| 1995 | 4 | 15 | 1 | 29.615 | 90 | 80 | 003 | 52 | 9999.9 | 9999.9 |
The type of hydrometeorological data and the name of the hydrometeorological data file are selected in the Continuous Simulation dialog box. WMS supports none of the hydrometeorological input data formats, and the hydrometeorological data must be assembled in software external to WMS. It is highly recommended that hydrometeorological data be converted to the WES format before use in the GSSHA model.
Missing data
In the case of missing data, the ND code, as described above, should be entered in the data set. One line of data is required for each hour of the simulation. Do not skip hours or leave blank values in a line. If no data are present, enter the Year, Month, Day, Hour, and the appropriate ND code for each missing variable for each missing hour. Upon encountering the ND codes, GSSHA fills in missing data in the following way:
- In the case of missing pressure, total sky cover, wind speed, and dry bulb temperature, the last recorded readings are used until actual data resumes.
- For parameters with a strong diurnal pattern, such as air temperature, relative humidity, and global and direct radiation, missing hourly values are replaced with the last good value at the same time of day. For extended no data periods, the last values from the last good day of measurements are repeated until actual data resumes.
It is important that the hydrometeorological data set begin with at least one full day of complete data; no ND codes may be present.
Many stations have no radiation data. If no radiation data are available, GSSHA will calculate radiation based on the latitude and longitude of the watershed and the time of day. The latitude/longitude and time deviation from GMT is specified in the Continuous Simulation dialog box.
Rainfall data
The Rainfall data file for long-term simulations is comprised of a series of single storm events, as described in Chapter 9. An example of a two-storm long-term rainfall file is shown below. The GSSHA User’s Manual (Downer and Ogden in preparation) should be consulted for additional information on constructing rainfall files.
As shown in this example, it is possible to change the location and number of gages among storm events, as well as the type of rainfall. However, rainfall types cannot be mixed within a rainfall event.
Modeling the Unsaturated Zone with Richards' Equation
Modeling of the unsaturated zone is a key addition of the GSSHA model. Richards’ equation is currently the most complete method to simulate soil water movement in the unsaturated zone. When Richards’ equation is solved in GSSHA to calculate soil moistures and soil water movement, infiltration, actual evapotranspiration, and groundwater recharge are also calculated as part of an integrated solution. Because most soil water movement is in the vertical direction, a 1-D representation of the soil column is employed to simulate the unsaturated zone. The GSSHA representation of the soil column is shown in Figure 21. As shown in this figure, when using Richards’ equation to represent the unsaturated zone, the soil column is subdivided in to three layers: A, B, and C horizons. Parameters must be specified for each of these three layers. Unlike the Green and Ampt based models of infiltration, Richards’ equation is a partial differential equation that must be solved numerically. Therefore, each of the soil layers must be subdivided into cells. The user must specify the cell size of each layer, along with the hydraulic properties of the soil.
To use Richards’ equation, several global and distributed parameters must be set. The global parameters are related to the numerical solution of Richards’ equation. The distributed parameters describe the soil and are similar to the parameters used in the Green and Ampt approaches.
Richards’ equation is selected from the GSSHA Job Control Parameters dialog under the Infiltration options.
Global parameters
The global parameters for Richards’ equation are set from the GSSHA Job Control Parameters dialog under the Infiltration options. With Richard’s infiltration toggled on, hit the Edit Parameters... button to access the global parameter list. The global parameters are:
- Weight – Fraction between 0.0 and 1.0 (dimensionless). This is the weighting factor used to calculate inter-cell hydraulic conductivities when using an arithmetic mean to calculate the inter-cell hydraulic conductivities. Use 1.0 for forward weighting, 0.0 for backwards, and 0.5 for central. The default value is 1.0
- DTHETA Max – Fraction between 0.0 and the porosity of the soil (m^3/m^3), the maximum allowable water content change in any finite difference cell during a single time-step. Typical range is between 0.002 and 0.030 (Belmans, Wesseling, and Feddes 1983). The default value is 0.025.
- C Option – Brooks or Havercamp sets the curves used to define the relationships between water content and soil suction, pressure, and water content and hydraulic conductivity. An example of the curves for a typical clay and sand are shown in Figure 22. The user is referred to the GSSHA User’s Manual for more detailed information on this topic. The default value is Brooks.
- K Option – (Arithmetic or Geometric) method used to calculate inter-cell hydraulic conductivities.
- Upper Option – method used to determine the hydraulic conductivity at the soil surface during ponded water conditions; the options are Normal, Green Ampt, and Average. Normal specifies that the normal cell-centered value of hydraulic conductivity be used, Green Ampt specifies that the saturated hydraulic conductivity of the soil in the cell be used, and Average specifies that an average of the two be used. The default value is Normal. For more information, see the GSSHA User’s Manual.
- Max Iteration – the maximum number of iterations each time-step to determine water capacity and hydraulic conductivity. The typical range is 1 to 10 iterations. The default value is 1.
- Max Num – integer value, maximum number of cells in any unsaturated soil column.
Distributed parameters
As with all distributed parameters, the distributed parameters for the Richards’ equation are assigned using index maps and the mapping tables as described in Chapter 5. Assignment of parameters with Richards’ equations differs from the other processes in that for each different soil type in the index map, three soil layers must be defined. Parameters and discretization must also be assigned for all three layers. The parameters that must be defined depends on which option is used to define the PCS curves, Brooks or Havercamp. The Havercamp formulation is best if laboratory data are available to fit the needed parameters as detailed below (Figure 22). Testing by Downer (2002) showed that the Havercamp equations could best define the soil behavior. If no detailed data exist, as is typical, then the Brooks and Corey (1964) method may be used and the parameters needed for the Brooks and Corey model can either be measured or estimated from soil textures and literature sources such as Rawls, Brakensiek, and Saxton (1982).
Parameters for the Richards’ equation are assigned in the GSSHA Mapping Table Editor. For the Brooks and Corey method, the following parameters are assigned for each of the three layers.
- Hydraulic Conductivity –saturated hydraulic conductivity of the soil describes the rate water will enter the soil under unit head and saturated conditions (cm/hr) .
- Porosity - volume of voids/total volume of soil, fraction between 0.0 to 1.0 (m3/m3).
- Residual saturation –water content of air dry soil, fraction between 0.0 to 1.0 (m3/m3).
- Wilting point – fraction between residual saturation and porosity, water content below which plants cannot uptake water from the soil (m3/m3).
- Depth – thickness of the soil layer (cm). Should be rounded up or down to nearest centimeter.
- Lambda – pore distribution index (cm/cm). Describes the straight line length to the soil water path length.
- Bubbling pressure – pressure at which air enters the soil column (cm). Must be negative.
- Delta Z – vertical cell size of the layer (cm). Should be evenly divisible into the depth of the layer.
For the Havercamp method, the following parameters must be specified for each of the three layers. Parameters from the Havercamp method must be determined from field or laboratory testing.
- Hydraulic Conductivity –saturated hydraulic conductivity of the soil (cm/hr) describes the rate water will enter the soil under unit head and saturated conditions.
- Porosity - volume of voids/total volume of soil, fraction between 0.0 to 1.0 (m3/m3).
- Residual saturation –water content of air dry soil, fraction between 0.0 to 1.0 (m3/m3).
- Wilting point – fraction between residual saturation and porosity, water content below which plants cannot uptake water from the soil (m3/m3).
- Depth – thickness of the soil layer (cm). Should be rounded up or down to nearest centimeter.
- Alpha – factor fitted from field or laboratory data.
- Beta – factor fitted from field for laboratory data.
- AHAV – factor fitted from field for laboratory data.
- BHAV - factor fitted from field for laboratory data.
- Delta Z – vertical cell size of the layer (cm). Should be evenly divisible into the depth of the layer.
Soil depth and discretization
The soils in the unsaturated zone need to be defined down to a depth that includes the active region of the soil, where the water content experiences large changes in value. This should include the root zone. Typically, soil surveys describe the A, B, and C soil horizons of soils in the study region. In lieu of field measurements, these surveys provide information on the appropriate thicknesses of each of the soil layers for the Richards’ equation model. While Downer (2002) showed that the GSSHA model is not sensitive to the depth of the soil layer, it is best to err on the conservative side and make the soil columns deeper than necessary. As this will increase the computation time, it may be useful to experiment with the soil layer depths to reduce the amount of soil being simulated, if possible. When the saturated zone is the lower boundary, the area between the defined soil column and the water table will be assigned the parameters used in the third, C, layer, and the cells will be the size specified in the WMS subsurface parameters dialog found in the job control options.
The other big consideration in application of Richards’ equation is the cell discretization. Essentially, the smaller the cells the better the answer, but the longer the simulation time. Very small cells, 1 cm or less, will typically be required in the top 10 cm of the soil column (van Dam and Feddes 2000; Downer 2002). Much larger cells may be used at depth in the soil column. Increases in the cell size between layers should be gradual.
Modeling Two-dimensional, Saturated, Lateral Groundwater Flow
Two-dimensional, saturated, lateral groundwater movement may be simulated in GSSHA. The purpose of simulating 2-D, lateral groundwater movement is to provide the effects of saturated groundwater on surface water processes, such as influences on soil moisture, infiltration, and ET, location of saturated source areas and seeps, and stream/groundwater interactions. The saturated groundwater modeling option is intended to be used in conjunction with Richards’ equation modeling of the unsaturated zone. When 2-D saturated groundwater is coupled to the Richards’ equation, the 1-D unsaturated model sits on top of the moving water table, which becomes the lower boundary condition for the unsaturated zone solver (Figure 21). The unsaturated model provides recharge (positive or negative) to the unsaturated zone.
When conducting long-term simulations (Chapter 10), it is also possible to use the GAR model of infiltration to provide estimates of groundwater recharge for the 2-D lateral groundwater solution. However, this option does not provide many of the advantages of coupling Richards’ equation to the 2-D lateral groundwater model, such as the effect of groundwater on soil moistures in the unsaturated zone. This approach is intended for simple problems and where a more qualitative result is acceptable, and has been applied as such. Downer et al. (2002b).
Global parameters
Global parameters for 2-D saturated flow modeling are specified by toggling on Subsurface in the GSSHA Job Control Parameters dialog. This produces the Subsurface Parameters dialog box where the following parameters may be specified.
- Time-step – groundwater model time-step (s). Typically the groundwater time-step may be much larger than the overall model time-step, typical values are 300 - 1,200 sec. The groundwater time-step must be equal to or larger than the overall model time-step, and the overall model time-step must be integer divisible into the groundwater model time-step. During rainfall events, the groundwater model time-step is temporarily changed to the overall model time-step, and then changed back at the end of channel routing and overland flow routing. This switching is handled internally.
- LSOR direction – The solution technique currently used to solve the 2-D groundwater free surface flow equations is line successive over relaxation (LSOR) (for example Tannehill, Anderson, and Pletcher 1997). When LSOR is applied, the solution is either by rows or by columns. The solution should be aligned with the principal direction of saturated groundwater flow. The options are either Vertical or Horizontal, which indicates that your principal direction of flow is in the vertical direction, along the y axis, or in the horizontal direction, along the x axis.
- LSOR convergence – LSOR is an iterative method. The user must supply a convergence criteria. The criterion is in meters of groundwater head or depth. The default value, 10-5, is typically sufficient for a good solution. Stricter criteria may lead to slower solutions, or nonconvergence.
- Relaxation – The relaxation coefficient is used to project the current solution out into the future in an attempt to speed up convergence. A value of 1.0, the default, indicates no projection. Values greater than 1.0 indicate that projections into the future are desired. Values up to 1.5 may speed the groundwater model solution. Typically, a value of about 1.2 provides the fastest solution. Increasing the relaxation coefficient to greater than 1.0 can result in nonconvergence of the solution. If this happens, the relaxation coefficient should be reduced. It is sometimes necessary to reduce the relaxation coefficient to less than 1.0 to obtain convergence of the solution.
- Leakage rate – this is the leakage rate (cm/hr) through the bottom of the aquifer. This is a uniform value that is applied to every cell in the grid. The default value is 0.0.
- Define initial moisture – when this option is toggled on, it means you wish to use the values of initial moisture of cells in the unsaturated zone as entered in the mapping table. Otherwise, the default, initial soil moistures in the unsaturated zone are assumed to be the water contents that correspond to soil pressures in equilibrium with the saturated groundwater elevation.
Distributed parameters
Unlike many of the other distributed parameters assigned to each cell, distributed groundwater modeling parameters are not assigned using the mapping tables and index maps. All distributed parameters for the groundwater model are assigned with the Continuous Maps... dialog, selected in the GSSHA menu. The values for the continuous maps may be imported as GRASS or Arc/Info gridded data, may be assigned a constant value, may be assigned from an index map, or may be manually entered using the spreadsheet in the Continuous Maps dialog box.
To import any required data, select Import, toggle on the gridded data type, GRASS ASCII grid file or Arc/Info grid file, and then select the name of the file to be imported. To assign values using an index map, select Index Map -> Array, and select the name of the index map you wish to use. The Reclassify Options may then be used to assign all the necessary groundwater parameters from the assigned Index map or maps. The Constant -> Array option may also be used to assign a uniform value of any parameter. Finally, any and all of the values of parameters may be entered or edited manually in the spreadsheet. The distributed parameters that must be entered are:
- Aquifer bottom – elevation of the aquifer bottom (m).
- Water table – initial values of groundwater elevation (m).
- GW hydraulic conductivity – value of horizontal hydraulic conductivity in the saturated zone (cm hr-1).
- GW porosity – value of porosity of the saturated media, fraction of voids (m3/m3).
Boundary conditions
Solution of the 2-D, lateral flow, saturated groundwater equations requires that boundary conditions be assigned to every cell in the grid. A boundary condition map must be created that assigns an integer value representing the boundary condition to every cell.
Boundary conditions are assigned from the Map Module. The coverage is set to GSSHA Boundary Condition from the Coverages dialog box under the Feature Objects menu. Boundary conditions are established from feature points or arcs. The points or arcs are created over the grid cells to assign a boundary, and the type of boundary condition is selected from Attributes ... under Feature Objects menu. The option of which type of boundary conditions can be assigned as Attributes... depends on whether a feature node or arc is selected.
The following boundary conditions can be assigned:
- No-flow
- Regular infiltration cell (no special boundary condition)
- Specified head
- Dynamic flux, well (not currently active in GSSHA)
- Stream cell with calculated flux between stream node and groundwater cell
- Stream cell with a specified head
- Static flux (well)
No-flow
This boundary type is typically assigned along the watershed boundary or along portions of the watershed boundary. This boundary condition represents a region where no lateral groundwater flow is permitted. When no-flow arcs are located along the watershed boundary, this is referred to as a groundwater divide. All cells not within the active watershed are no-flow boundary cells. No-flow boundaries are assigned with feature arcs.
General
The general type specifies that the cell is a regular infiltration cell, indicating no special boundary is desired. The general boundary condition is the default option. General boundaries can be assigned with either feature nodes or arcs.
Constant head
A constant head boundary indicates that the groundwater level in that cell remains constant for the duration of the simulation. The value for the head boundary is taken from the initial values assigned with the water table map (See above). Specified heads are normally applied along the watershed boundary where known values of head exist. They may be assigned with either a feature node or arc.
Dynamic well
This boundary indicates that a dynamic, temporally varying, pumping well exists in the cell. They may be assigned with feature nodes. This option is not currently supported by GSSHA.
Flux river
This boundary condition indicates that the cell contains a stream node and the flux between the stream node and saturated groundwater below the stream node be calculated based on Darcy’s law, as described by McDonald and Harbaugh (1988), allowing an exchange of water between the stream and groundwater during every groundwater update. These boundaries are assigned with feature arcs.
When assigning flux river boundaries to a cell, the thickness of the bed material, M river (cm), and the hydraulic conductivity of the bed material, K river (cm/hr), must be assigned to the stream network as Attributes... to the GSSHA coverage. Only trapezoidal stream sections may be specified as flux river boundaries.
Head river
Another possible boundary condition for cells containing stream nodes is a head boundary condition, head river. This boundary condition indicates that for the purposes of the saturated groundwater simulations, the cell will behave as a constant head cell and will not be updated during the saturated groundwater calculations. The value of the head in the cell is set to be the elevation of the water surface in the stream node above the cell. In this case, the stream cell influences the groundwater calculations, but the groundwater calculation does not influence the stream calculations.
Static well
A static well boundary means that the cell will have a source/sink term of constant rate, m3×d-1. These boundaries are assigned with feature nodes. Select, or create and select, the node where the static pumping well is to be located. Select Feature Objects -> Attributes. Select static well from the drop down list and type in the pumping rate in the box labeled Pumping rate. Groundwater extractions have a positive sign; injections have a negative sign.
Running GSSHA
Running GSSHA from WMS
You can launch the GSSHA model directly from WMS by choosing the Run GSSHA command from the GSSHA menu. WMS uses the executable for GSSHA that is specified in the Models tab of the Preferences dialog. If WMS cannot find the GSSHA executable, then you will be prompted to locate the file separately using a file browser.
WMS passes the current project file to GSSHA, and you have the opportunity to let WMS write the project file prior to launching GSSHA. If you have already saved the project file and no changes have been made since saving, it is not necessary to write the project file again. If you have made modifications to your simulation since last saving the project file, you should turn on the toggle box to write the project file before running GSSHA so that all changes are saved to the project file.
Running GSSHA from command line
GSSHA can also be run from the command line using the project file as the sole command-line argument. For example, from a command prompt window you would type:
- gssha simulate.prj
where simulate.prj is the name of the project file saved from WMS and resides in the same directory as GSSHA.exe. You may also use the Start -> Run command from Windows.
If the project file is not in the same directory as GSSHA.exe, you must enter the full path name to the project file (i.e., C:\mysimulations\simulate.prj) in order for GSSHA to run successfully. Often it is best to copy the GSSHA.exe file to the directory where the project has been saved.
Project file
The project file definition is made up of a series of cards followed by parameter(s) (usually a file name) related to that card. For example, the watershed mask is defined on a single line using the card WATERSHED_MASK followed by the name of the file containing the watershed mask. The project file informs GSSHA which simulation options (e.g., overland flow, infiltration, long-term, etc.) to perform along with all of the necessary parameters required for the desired options. An example project file is shown below:
GSSHAPROJECT WMS 7.0 WATERSHED_MASK bear2.msk FLINE bear2.map METRIC GRIDSIZE 30.000000 ROWS 61 COLS 76 TOT_TIME 480 TIMESTEP 5 OUTROW 41 OUTCOL 74 OUTSLOPE 0.001000 MAP_FREQ 360 HYD_FREQ 180 MAP_TYPE 2 CHAN_EXPLIC SED_POROSITY 0.400000 ELEVATION bear2.ele DEPTH bear2.dep CHANNEL_INPUT bear2.cip LINKS bear2.lks NODES bear2.nod DIS_PROFILE bear2.qpf WAT_SURF_PROFILE bear2.wpf OVERTYPE ADE GREEN_AMPT MAPPING_TABLE bear2.cmt MATERIALS bear2.mat SUMMARY bear2.sum OUTLET_HYDRO bear2.hyd OUTLET_SED_FLUX bear2.sed PRECIP_UNIF RAIN_INTENSITY 20.000000 RAIN_DURATION 120 START_DATE 1994 1 1 START_TIME 12 0
For a complete description of all the cards and their related parameter(s), see the GSSHA User’s Manual (Downer and Ogden in preparation).
Post-Processing
GSSHA can produce a variety of outputs for the user. GSSHA automatically outputs a run summary file, which has the extension .sum, and an outlet hydrograph file, which has the extension .hyd. GSSHA can also output time series data for a number of variables at any point in the channel network and in the 2-D grid. GSSHA can produce a series of maps that can be displayed in WMS containing surface depth and/or other results. Once the simulation has been completed, results can be read back into WMS as a solution for post-processing. This chapter discusses the different output options available from GSSHA and a few of the methods available in WMS for viewing these computed results.
Output control
In WMS the output map choices are specified from the Output Control dialog accessible only from within the Job Control dialog. Since the computational time-step is generally small compared to the overall simulation time, a value representing the time between saving of results data may be defined. This time parameter determines the frequency of writing output raster maps or data sets. The time is measured in units of minutes.
Data set map options
The data set map output options are selected, along with the output frequency, with Write Frequency, and the type of map to output, with Type. The output maps can be a WMS data set in binary or ASCII format, or a series of GRASS ASCII maps. Since this primer accompanies WMS, it will be assumed that the data set option is turned on throughout the rest of the primer.
The different data set maps supported by WMS that may be saved for a given simulation include:
- Distributed rainfall intensity (mm h-1)
- Surface depth (m) - displays channel depth in channel cells if channel routing is performed
- Cumulative infiltration depth (m) – (infiltration must be turned on for the simulation)
- Surface soil moisture - soil volumetric water content
- Infiltration rate (cm h-1) - infiltration must be turned on for the simulation
- Channel depth (m)
- Channel discharge (m3s-1)
- Volume of suspended sediments (m3)
- Maximum sediment flux (m3s-1)
- Net sediment volume (m3)
- Groundwater head (m)
Additional maps may be created by specifying the appropriate cards in the project file, as described in the GSSHA User’s Manual.
Data tree
The data tree is a new feature in WMS 7.1. It serves as a means of organizing all the data sets associated with the several models and modules in WMS. In the 2D Grid module, the data tree serves to store and modify the attributes of all gridded data sets. In this capacity is replaces the data browser dialog in WMS 6.1. However, it can do much more than the data browser did.
Data Sets
The data tree serves as a manager for all of the gridded data sets and link / node data sets that have been read into WMS. When other modules are active the data tree references TINs, DEMs, Scatterpoint sets, Coverages, and other data storage types. The main strength of the data tree lies in consolidating access to the data sets. Right-clicking on a data set brings up a list of options that are available for that data type. In the 2D Grid module, when a data set is right-clicked, a right-click menu comes up that offers the following options: exporting the data set, renaming the data set, viewing the properties of the data set, viewing the values of the data set, setting the contour options for the data set, and setting the data set to be the elevation data set.
Index Maps
Unique to GSSHA are special data sets that serve as index maps that link simulation parameters to their spatial distribution. The principle means of modifying and creating index maps is in the Index Map dialog but the index maps are now also able to be accessed through the data tree. When an index map has been created or read into WMS a folder appears in the data tree, named Index Maps, that contains all of the index maps for the simulation. Index maps can then be treated like regular data sets; they can be contoured, renamed, deleted, and edited.
Solutions
While solutions are not new to GSSHA, being able to work with them in WMS is a new feature. Accessible from the GSSHA menu in the 2D Grid module is the command Read Solution... which looks for a GSSHA project file and then reads in all of the associated data sets and lumps them together into a solution folder in the data tree. Solution folders are identified by a lowercase “s” on the folder. All of the data sets in the folder are treated as regular data sets. Organizing the data sets into a solution allows several solutions to be in memory at the same time. Several dialogs look for solutions and the associated data sets to set up and display output graphs. Along with the regular data sets, the summary file for the project is also accessible for each solution by double-clicking the summary file tree item under the solution folder.
Individual solution output time series data for a cell may be viewed from the Solution Results dialog accessed from the Feature Point/Node Type dialog. This dialog will only show the output data set time series for the cell that underlies the feature point selected. To compare the solution output at a cell with observed data, select the Observations button on the Feature Point/Node Type dialog.
Contour Options
New to WMS 7.1 is the use of OpenGL code for much better graphics display. OpenGL is a 3D graphics library that makes displaying graphics in WMS much faster and more efficient. The grid display routines in WMS have been enhanced with a better interpolation scheme that allows for a much smoother grid display as well as taking advantage of the strengths of OpenGL. The contouring routines have been redone to also use the enhanced grid and OpenGL, which results in faster, smoother surfaces that are continuous color contoured as opposed to step color contoured as in WMS 6.1. Also, OpenGL shades surfaces automatically, so this option is always turned on when the contour is color filled.
Cell filling the grid has been an option since WMS 6.1. However, WMS 7.1 allows much more flexibility in visualizing the output and input to GSSHA through cell filling by making it into part of the contour options. Simply make sure the cell filled radio button is selected and each cell will be filled with the color that represents the data point at the center of the cell. This color is taken from a smooth (linearly interpolated) color ramp. Cell filling is independent of block-style cell display, which is set in the display options.
One of the new features of the data tree is that it allows access to individual contour options for each data set. When a data set is read in it is given the default set of contour options that can then be modified by right clicking on the data set in the data tree. Whichever data set is active is the only data set contoured. The contours for the grid come from the active data set whereas the elevations of the grid come from the current elevation data set. This setup allows the results of a GSSHA simulation to be displayed as contours on a grid that is shaped like the underlying terrain. In the data tree the active data set is shown with a yellow icon and bold lettering and the current elevation data set has (elev) after the name of the data set.
Visualizing results
Contouring
Turning on the contour option allows any data set to be contoured. Contours options are set for any gridded data set by right-clicking on the data set and selecting Contour Options. An option for gridded data sets is cell fill contouring. The cell fill contouring fills the entire grid cell with the same color according to its computed function value. The Contour Options dialog can be used to control all of the different available options. The Color Ramp Options are used to specify the coloring scheme of contours and whether or not a legend of values is drawn. More information on contouring can be found in the WMS Help File (Nelson 2005).
Animations
Animation sequences are created in WMS’s Film Loop dialog using a series of saved images. Prior to running an animation, the Setup dialog should be brought up so that the size of images, number of time-steps, and other display parameters can be set. Upon exiting the Setup dialog, an image for each time-step of the animation is created. After all images have been created, they can be played back using the VCR-like controls of the Film Loop dialog. Animation files may be saved as AVI files so that subsequent runs do not require the setup process but can simply be read into the Film Loop dialog or run in any standard AVI players.
References
Bras, R. L. (1990). Hydrology: An introduction to hydrologic science. Addison-Wesley, Reading, MA, 643.
Belmans, C., Wesseling, J. G., and Feddes, R. A. (1983). “Simulation model of the water balance of a cropped soil: SWATRE,” J. Hydrol. 63, 271-286.
Brigham Young University (BYU). (1997a). Watershed Modeling System WMS Version 5.0 reference manual. Brigham Young University, Provo, UT.
__________. (1997b). Primer, Using WMS for CASC2D data development, for use with CASC2D 1.17 and WMS 5.0. Brigham Young University, Provo, UT.
Brooks, R. H., and Corey, A. T. (1964). Hydraulic properties of porous media, Hydrology Papers, 3, Colorado State University, Fort Collins, CO.
Deardorff, J. W. (1977). “A parameterization of ground surface moisture content for use in atmospheric prediction models,” J. Appl., Meteor. 16, 1182-1185.
Doe, W. M., and Saghafian, B. (1992). “Spatial and temporal effects of army maneuvers on watershed response: The integration of GRASS and a 2-D hydrologic model.” Proc. 7th Annual GRASS Users Conference. National Park Service Technical Report NPS/NRG15D/NRTR-93/13, Lakewood, CO, 91-165.
Downer, C. W. (2002). “Identification and modeling of important stream flow producing processes in watersheds,” Ph.D. diss., University of Connecticut.
Downer, C. W., and Ogden, F. L. “GSSHA User’s Manual,” U.S. Army Engineer Research and Development Center (in preparation), Vicksburg, MS.
Downer, C. W., Ogden, F. L., Martin, W., and Harmon, R. S. (2002a). “Theory, development, and applicability of the surface water hydrologic model CASC2D,” Hydrol. Pro. 16, 255-275.
Downer, C. W., James, W., Byrd, A., and Eggert, G. (2002b). “Gridded surface subsurface hydrologic analysis (GSSHA) model simulation of hydrologic conditions and restruction scenarios for the judicial Ditch 31 Watershed, Minnesota,” Water Quality Technical Note AM-12, U.S. Army Engineer Research and Development Center, Vicksburg, MS.
Downer, C. W., Nelson, E. J., and Byrd, A. (2002). “Primer: Using Watershed Modeling System (WMS) for Gridded Surface Subsurface Hydrologic Analysis (GSSHA) Data Development—WMS 6.1 and GSSHA 1.43C,” ERDC/CHL TR-02-XX,
U.S. Army Engineer Research and Development Center, Vicksburg, MS.Engman, E. T. (1986). “Roughness coefficients for routing surface runoff,” ASCE, Journal of Irrigation and Drainage Engineering.112(1), 39-52.
Gray, D. M. (1970). Handbook on the principles of hydrology. National Research Council of Canada, Water Information Center Inc., Water Research Building, Manhasset Isle, Port Washington, NY.
Green, W. H., and Ampt, G. A. (1911). “Studies of soil physics: 1. Flow of air and water through soils,” J. Agric. Sci. 4, 1-24.
Horton, R. E. (1933). “The role of infiltration in the hydrologic cycle, American Geophysical Union,” Transactions 14, 446-460.
Johnson, B. E. (1997). “Development of a storm event based two-dimensional upland erosion model,” Ph.D. diss., Dept of Civil Engineering, Colorado State University, Fort Collins, CO.
Julien, P. Y. (1995). Erosion and sedimentation. Press Syndicate of the University of Cambridge, New York, NY.
Julien, P. Y., and Saghafian, B. (1991). A two-dimensional watershed rainfall-runoff model - User’s manual, Center for Geosciences, Colorado State University, Fort Collins, CO, 66.
Julien, P. Y., Saghafian, B., and Ogden, F. L. (1995). “Raster-based hydrologic modeling of spatially-varied surface runoff,” Water Resources Bulletin, AWRA, 31(3), 523-536.
Kilinc, M., and Richardson, E. V. (1973). “Mechanics of soil erosion from overland flow generated by simulated rainfall,” Hydrology Papers No. 63, Colorado State University, Fort Collins, CO.
Martz, L. W., and Garbrecht, J. (1992). “Numerical definition of drainage network and subcatchment areas from digital elevation models,” Computers and Geosciences 18(6), 747-761.
McDonald, M. G., and Harbaugh, A. W. (1988). “A modular three-dimensional finite-difference ground-water flow model, Book 6, Chapter A1,” Techniques of Water-Resources Investigations of the United States Geological Survey, U.S. Geological Survey.
Monteith, J. L. (1965). “Evaporation and environment,” Symp. Soc. Exp. Biol. XIX, 205-234.
__________. (1981). “Evaporation and surface temperature,” Q. J. R. Meteorol. Soc. 107, 1-27.
Nelson, E. J. (2001). “WMS Ver. 6.1 HTML Help Document,” Environmental Modeling Research Laboratory, Brigham Young University, Provo, UT.
Nelson, E. J. (2003). “WMS Ver. 7.0 HTML Help Document,” Environmental Modeling Research Laboratory, Brigham Young University, Provo, UT.
Nelson, E. J. (2005). “WMS Ver. 7.1 HTML Help Document,” Environmental Modeling Research Laboratory, Brigham Young University, Provo, UT.
Ogden, F. L. (2000). CASC2D Reference manual, version 2.0, Department of Civil and Environmental Engineering, University of Connecticut.
Ogden, F. L., and Julien, P. Y. (1994). “Runoff model sensitivity to radar-rainfall resolution,” J. of Hydrology 158, 1-18.
___________. (2002). “CASC2D: A two-dimensional, physically-based, hortonian, hydrologic model,” mathematical models of small watershed hydrology and applications, ISBN 1-887201-35-1, V. J. Singh and D. Freverts, eds., Water Resources Publications, Littleton, CO, 972.
Ogden, F. L., Saghafian, B., and Krajewski, W. F. (1994). “GIS-based channel extraction and smoothing algorithm for distributed hydrologic modeling.” Proc. Hydraulic Engineering `94, ASCE Hydraulics Specialty Conference, G. V. Cotroneo and R. R. Rumer, eds., August 1-5 1994, Buffalo, NY, 237-241.
Ogden, F. L., and Saghafian, B. (1997). “Green and ampt infiltration with redistribution,” J. Irr. and Drain. Engr. 123, 386-393.
Ogden, F. L., Sharif, H. O., Senarath, S. U. S., Smith, J. A., Baeck, M. L., and Richardson, J. R. (2000). Hydrologic analysis of the Fort Collins, Colorado, flash flood of 1997,” J. Hydrol. 228, 82‑100.
Pinder, G. F., and Bredehoeft, J. D. (1968). “Application of a digital computer for aquifer elevations,” Wat. Resour. Res. 4, 1069-1093.
Ponce, V. M. (1989). Engineering Hydrology Principles and Practices. ISBN 0-13-277831-9, Prentice Hall, Englewood Cliffs, NJ, 640.
Rawls, W. J., Brakensiek, D. L., and Miller, N. (1983). “Green-Ampt infiltration parameters from soils data,” ASCE J. Hyd. Engr. 109(1), 62-70.
Rawls, W. J., Brakensiek, D. L., and Saxton, K. E. (1982). “Estimation of soil water properties,” Trans. of ASAE. 1316-1320.
Ree, W. O., Wimberley, F. L., and Crow, F. R. (1977). “Manning n and the overland flow equation.” Trans. of the ASCE. 89-95.
Richards, L. A. (1931). “Capillary conduction of liquids in porous mediums,” Physics 1, 318-333.
Saghafian, B. (1992). Hydrologic analysis of watershed response to spatially varied infiltration, Ph.D. diss., Civil Engr. Dept., Colorado State University, Fort Collins, CO.
__________. (1993). “Implementation of a distributed hydrologic model within Geographic Resources Analysis Support System (GRASS).” Proceedings of the Second International Conference on Integrating Environmental Models and GIS, Breckenridge, CO.
Senarath, S. U. S., Ogden, F. L., Downer, C. W., and Sharif, H. O. (2000). “On the calibration and verification of two-dimensional, distributed, Hortonian, continuous watershed models,” Wat. Resour. Res. 36(6), 1495-1510.
Smith, R. E., Corradini, C., and Melone, F. (1993). “Modeling infiltration for multistorm runoff events,” Water Resources Research 29(1), 133-144.
Tannehill, J. C., Anderson, D. A., and Pletcher, R. H. (1997). Computational fluid mechanics and heat transfer, 2nd ed., Taylor and Francis, Washington, DC.
Trescott, P. C., and Larson, S. P. (1977). “Comparison of iterative methods of solving two-dimensional groundwater flow equations,” Wat. Resourc. Res. 13(1), 125-136.
van Dam, J. C., and Feddes, R. A. (2000). “Numerical simulation of infiltration, evaporation, and shallow groundwater levels with the Richards equation, J. Hydrol. 233, 72-85.
Yang, C. T. (1973). “Incipient motion and sediment transport,” J. Hydr. Div. ASCE, 99, No. HY10:1679-1704.