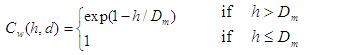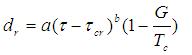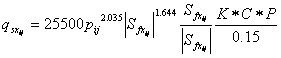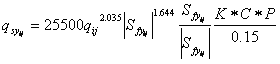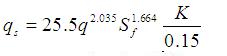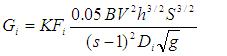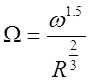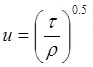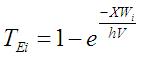Latest revision as of 14:02, 19 April 2008 (view source) Eshaw (talk | contribs)

(No difference)

---

Latest revision as of 14:02, 19 April 2008

10.1 Overland Erosion Formulation

10.1.1 Overland Erosion Controlling Equation

The overland sediment routing is based on a two-dimensional mass balance equation,

(96)

where h = water depth (m); c = sediment concentration (kg m^-3); t = time (s), q_x and q_y = unit discharge in x- and y-directions, respectively (m²/s); and e(x,y,t) = sediment source/sink (kg m^-2• s^-1); q_z(x,y,t)=lateral sediment inflow to the channels (m^-2 s^-1). e(x,y,t) consists of two major sources, namely, soil detached by raindrop impact and soil detached by surface runoff (or deposition):

(97)

where d_i=soil detachment by rainfall impact (kg m^-2• s^-1) and d_r=soil detachment by surface runoff (kg m^-2• s^-1).

10.1.2 Detachment of Overland Sediment Particles

Detachment of overland sediment particles occurs due to two processes, detachment by rainfall impact, and detachment by surface runoff.

10.1.2.1 Detachment by Rainfall Impact

Following a similar approach presented by Wicks and Bathurst [1996] and Gabet and Dunne [2003], detachment by raindrops is considered to be a function of rainfall intensity. Raindrop detachment also takes into account factors such as “cushioning” by ponded surface water, ground cover, and plant interception.

(98)

where d_i = detachment capacity rate (kg m^-2 s^-1), K_I = soil erodibility factor for detachment by raindrop impact (J^-1), C_w = water depth correction factor, C_G = canopy cover factor, C_i = a cover-management factor, I = rainfall intensity (mm h^-1), and β = empirical coefficient related to rainfall intensity.

The calculation of water depth correction factor is based on the assumption that surface water depths greater than a critical depth protect the soil from raindrop impact erosion Wicks and Bathurst [1996]. The expression for the correction factor, C_w, is,

(99)

where h = water depth (m), and D_m = median raindrop diameter (m). The median raindrop diameter is determined from the Laws and Parsons [1943] equation:

(100)

10.1.2.2 Surface Runoff Detachment

Surface runoff detaches soil particles by exerting a shear stress that breaks the bonds between particles. Erosion in rills is lumped and described as gross rill erosion. Within a grid cell, rill erosion and flow are assumed to be uniformly distributed. The detachment capacity rate by surface runoff has the form:

(101)

where: d_r = detachment capacity rate (kg m^-2•s^-1), a and b are empirical coefficients, τ = the flow shear stress (Pa), τ_cr is the critical shear stress, G is the sediment load (kg m^-2 s^-1), and T_c is the sediment transport capacity of surface runoff (kg m^-2 s^-1). In the WEPP model, b is assumed equal to 1.0. Equation 101 provides an upper limit on the rate at which sediment that can be taken up by flowing water.

10.1.3 Sediment transport capacity of surface runoff

Transport of sediments on the overland flow plane is constrained by the ability of the water to carry sediments. Many researchers have investigated the process and have identified multiple equations that can be used to calculate this carrying capacity of the overland flow. Several of these have been implemented in GSSHA.

10.1.3.1 Kilinc Richardson Equation

Kilinc and Richardson studied the mechanics of overland soil erosion at Colorado State University Engineering Research Center in a flume 1.2 m deep, 1.5 m wide, and 4.9 m in length. Their investigation resulted in a sediment transport equation of uniform flow sheet and rill erosion on bare sandy soil. The original one-dimensional Kilinc-Richardson (1973) equation is:

(102)

where: the factor 25,500 is an empirical constant, is the sediment unit discharge (ton m^-1 s^-1) and q and S_o have previously defined. The form of Equation 102 is consistent with many sediment transport predictors, as reviewed by Julien and Simons (1985).

Julien (1995) modified the original Kilinc-Richardson equation to expand the applicability of the equation to non-uniform flow with consideration of soil and land-use specific factors:

(103)

where: K = soil erodibility factor, with values ranging from 0 to 1, C = soil cropping factor (0-1), and P = conservation factor (0-1).

The K, C and P factors are empirical coefficients with the same conceptual meaning as those used in the Universal Soil Loss Equation (Renard et al., 1991). The factor 0.15 in the denominator represents the maximum erosivity of the sand used in the original flume experiments. Equation 103 is applied within each model grid cell in two dimensions, which allows separate calculations of the potential sediment transport rate in the x- and y-directions:

(104)

(105)

with S_ƒx and S_ƒy defined using Equation 2, and p and q calculated using Equations 6 and 7, respectively.

The numerical approach in the current version of GSSHA is to apply the modified Kilinc and Richardson equations 104 and 105 to determine potential transport of sediment within each grid cell. The methodology is explained in detail in Johnson (1997) and Johnson et al. (2000). The potential sediment discharge in each of the two flow directions in each grid cell is calculated using the following two equations:

(106)

and,

(107)

In the current version of GSSHA, the three erosioin parameters K, C, and P, have been replaced with a single erosion parameter K, which represents the three original components, without the need to specify three different parameters for each grid cell. Reducing the number of parameters greatly facilitates calibration. The form of the equation used in GSSHA is currently:

(108)

where q_s is the sediment unit discharge (kg m^-1 s^-1), q is the unit discharge (m³ s^-1), S_f is the friction slope (-), and K is a combined factor(0-1) that consists of the combined influence of soil erodibility, vegetation, and land-use.

10.1.3.2 Engelund-Hansen Equation

The Engelund-Hansen [1967] relation is used to calculate sediment transport for each sediment size class and the resulting total transport is calculated by multiplying the proportion of the size in the parent material by the calculated rate.

(109)

where G_i is the volumetric sediment transport rate of i^th size fraction (m³ s^-1), K is the calibration coefficient (=1 for standard equation) (-), F_i is the proportion of i^-th faction in the parent material or deposited layer (-), B is the width of flow (m), V is the mean water velocity (m s^-1), h is the flow depth (m), S is the water surface slope (-), s is the specific gravity of i^th fraction (-), and g is the gravitational acceleration (m s^-2), is the sediment density (kg m^-3), is the water density (kg m^-3), D_i is the mean size of i^-th fraction (m). The factor 0.05 in the equation was developed from empirical data.

The suggested applicability of the Engelund-Hansen equation is for, where "D_N" is the grain size for which N% of sediment is finer by weight, and for sand-size sediments coarser than 0.15 mm.

10.1.3.3 Stream Power Approach

Several stream power methods [Everaert 1991] can also be chosen to calculate the transport capacity of surface runoff. The general expression has the form:

(110)

where a is the transport coefficient, b is an exponent, ω = steam power; ω_c=a critical stream power. Prior to version 5.7 these values were specified by the user. For versions 5.7 and beyond the exponents are assigned based on literature values [Everaert 1991]. These there parameters are no longer input in the cmt input table file.

10.1.3.4 Median size diameter, D₅₀ , Approach

In the versions 5.7s and beyond, the Stream Power Approach defined in 10.1.3.3, are replaced by laboratory physical model imperical equations derived by Everaert [1991] which are based on the sediment particle median size diameter, D50. The replacement is done to reduce the number of calibration parameters, a, b and critical values defined in sec. 10.1.3.3.

The followings are the list of methods and their respective equations:

a) Effective stream power method:

- (a1)

where,

- (a2)

- (a3)

and <math>q_s</math> = sediment unit discharge (kg/ m/ sec)

<math>D50</math> = Grain size parameter (um)

<math>\Omega</math> = effective stream power

<math>\omega</math> = stream power (N/m/s)

<math>R</math> = flow depth (m)

<math>q</math> = unit discharge (m²/s)

<math>S_f</math> = friction slope (m/m)

<math>\rho</math> = density of water at 20 C (kg/m³)

<math>g</math> = gravitational acceleration

This method is implemented if 4 is used for the project card SOIL_EROSION.

b) unit stream power method:

- (b)

where, <math>Vel</math> = velocity (m/s)

<math>S_f</math> = friction slope (m/m)

<math>q_s</math> = sediment unit discharge (kg/ m/ sec)

<math>D_{50}</math> = Grain size parameter (um)

This method is implemented if 3 is used for the project card SOIL_EROSION.

c) slope and unit discharge method:

if(d50<33.0)

- (c1)

else if(d50>=33.0 && d50<61.0)

- (c2)

else if(d50>=61.0 && d50<122.0)

- (c3)

else if(d50>=122.0 && d50<190.0)

- (c4)

If(d50>190.0)

- (c5)

This method is implemented if 5 is used for the project card SOIL_EROSION.

d) Transport capacity by shear velocity method:

- (d1)

u = shear velocity (m/s)

- (d2)

Τ = shear stress (N/m2)

if(d50<33) and if(u>1.4)

- (d3)

if(d50>=33.0 && d50<61.0) and if(u>1.4)

- (d4)

if(d50>=61.0 && d50<122.0) and if(u>1.45)

- (d5)

if(d50>=122.0 && d50<190.0) and if(shear_vel>1.55)

- (d6)

if(shear_vel>1.8)

- (d7)

In the above equations, D₅₀ and all other physically based hydrological, topographical and geomorphological parameters are defined by GSSHA model and need not be calibrated. As these methods are solely based on the experimental flume scale of 5 x 30 cm and 12 x 100 cm, the applicability of these lab model scale based imperical relations has been tested on catchment scale and a product of ‘constant factor’ and ‘adjustment factor’ is applied as a multiplier to each equation (a – d) in this section. Adjustment factor is a parameter for calibrating the individual equations. Constant factor is used to confine the bound of adjuistment factor between 0 and 1 while calibrating. Constant factor for each method is hard coded. We are currently assessing these methods. All of them may not appear in the next release version.

10.1.4 Deposition rate

When the sediment transport capacity is insufficient to transport the sediment in suspension within a grid cell, sediment is deposited. Sediment deposition in each grid cell is calculated for each size fraction using a trap efficiency relation [Johnson et al., 2000]:

(111)

where: T_Ei is the trap efficiency for the i^th size fraction, X is the width of the grid cell (m), W_i is the fall velocity of the i^th size fraction (m s^-1), h is the overland flow depth (m), and V is the overland flow velocity (m s^-1). The trap efficiency is a number between 0 and 1, which is assumed equal to the fraction of suspended sediment in each size fraction that is deposited in the grid cell. The use of trap efficiency forces larger particles to deposit before smaller particles.

10.2 Channel Sediment Transport Formulation

The present version of GSSHA employs the unit stream power method of Yang’s (1973) for routing sand-size total-load in stream channels. Unit stream power is defined as the product of the average flow velocity, U, and the channel slope S_o. The rate of work done per unit weight of water in transporting sediment is assumed directly related to the rate of work available per unit weight of water. Thus, the total sediment concentration or total bed-material load must be directly related to the unit stream power. The following relation gives the basic concept of Yang’s (1973) method:

(112)

where: C_s is the total concentration of sand-size sediment particles in motion, US_o is unit stream power (L/T), U_* is the shear velocity (L/T), ν = kinematic viscosity of the sediment-water mixture (L/T²), w = fall velocity of the sediment (L/T), d = particle diameter (L). With some mathematical and statistical manipulations with Buckingham’s π theorem, Yang (1973) derived an energy-based equation to estimate the total sand-size sediment concentration in the channel.

Only particles sizes larger than a user specified value for sand are transported in this manner. Smaller particles are assumed to be suspended, and not bedload, and are transported with the advection dispersion equation. The bed is assumed to be mobile, and the banks fixed. The bed can agrade or degrade to a user-specified maximum allowable depth(Figure 14).

Either trapezoidal or natural cross sections can be used. Trapezoidal channels degrade vertically into the crosshatched area in the Figure 14. Degradation continues and bed load is transported at the rate calculated with the Yang (1973) method until the maximum degradation is reached. During degradation the initial bed width is maintained and degradation is uniform across the width of the bed. If the channel aggrades, the trapezoidal cross-section is filled. If a channel link has aggraded, and then degrades, the degradation will occur uniformly over the bottom of the trapezoid until the original bed elevation is restored. Further degradation occurs vertically downward from the initial trapezoid bottom-width. If a channel, degraded below the original bed elevation begins to aggrade, sediment will accumulate uniformly in the rectangular degraded area below the original bed elevation. Once the bed aggrades beyond the original bed elevation, the entire width of the trapezoid is filled. Natural channels follow a similar pattern of agradation and degradation. The change in channel bed elevations is tracked during the simulation of the model and the final computed bed elevations are output in a file called "new_bed_elevations.txt". These new computed bed elevations are not used in the computations during the simulation unless you specify the "ADJUST_CHANNEL_BED", in which case the bed will be dynamically adjusted during the simulation, affecting all channel computations as the simulation proceeds.

In the channels size particles smaller than the user specified value of sand are assumed to be in suspension, and are transported as wash load. This treatment implies that the flow is turbulent, and the travel time to the outlet of the catchment is short compared to the settling time, such that particles do not settle in the channel network. This assumption, combined with no bank erosion, results in the channels being neither a source nor sink of fines. Routing of suspended fines is a natural extension of the explicit diffusive-wave channel routing method. Suspended fine sediments are routed as concentrations. The concentration changes as a function of gradients in both concentration and velocity.

10.3 Applicability of the Sediment Routing Methods

Ogden and Heileg (2001) performed a detailed study on the performance of the methods used in the CASC2D version 1.18 model and early versions of the GSSHA model and model and made several reccomendations to improve the formulation. Many of these formulation enhancements have included in the current version of GSSHA, v4 and higher. Additional features include the ability to specify the number, size, and specific gravity of particles, sediment detachment due to rainfall impact, refinement of the Kilinc Richardson model, and the addition of several other methods of computing transport capacity. This model has been tested against historical data sets and demonstrates improved capability over earlier versions of the model. Of note is that all sediment transport capacity equations in GSSHA contain some type of "erodibility" factor that varies betweend zero and unity. These factors are typically assigned according to land use and include the effect of many processes and contributing factors. Proper assignment of the erodibility relies on calibrating the factors with observed data. Calibrated model parameters should also be verified with independent observed data not used in the calibration effort.

10.4 Simulations with Soil Erosion

10.4.1 General

A detailed report on the soil erosion methods, estimated parameter values, and testing is available here Sediment Tech Note. Soil erosion simulations are specified with the SOIL_EROSION project card. The SOIL_EROSION card is also used to select the transport equation to be used, with an integer value of 1-6. The six transport capacity options currently are:

1 - Engelund-Hansen
2 - Kilinc Richardson
3 - Unit stream power - replaces generalized stream method formulation, new for version 5.7 and beyond
4 - Effective stream power, new for v5.7
5 - Slope and unit discharge, new for v5.7
6 - Shear stress, new for v5.7

It should be noted that methods 3,4,5, and 6 replace a generalized "stream power" method, no longer in the model. The parameters used in the generalized "stream power" method are no longer input for versions 5.7 and beyond. The following information is annotated for this change in the model.

Soil and erosion properties are assigned with the use of the Mapping Table, Chapter 11. For GSSHA versions 5.7 and up, the first three variables are not used and should not be included in the table. The eight variables are input in the following order:

 
Transport Capacity Coefficient - no longer used
Transport Capacity Exponent - no longer used
Transport Capacity Critical Value - no longer used
Rain Splash Detachment Erosion Coefficient
Overland Detachment Coefficint
Overland Detachment Exponent
Overland Detachment Critical Value
Overland Transport Capacity Erosion Coefficient

Additional optional inputs and outputs are also available. These are described in detail in Section 3.10. If channel routing is not specified in the project file only overland soil erosion calculations are performed. Sediment transport can be simulated in either event or long-term simulation mode.

There are three general categories of parameters to enter into your mapping tables when running a sediment transport simulation. These categories of parameters are explained as follows:

10.4.1.1 Overland Sediment Particle Detachment Parameters

In the formulation used in GSSHA, overland sediment particle detachment is caused in two ways: by rainfall impact detachment and by surface runoff detachment. The following input parameters are used to control how much sediment is detached by these two methods:

Rainfall Impact Detachment

Rain splash detachment coefficient (SPLASH_K)

Surface Runoff (Rill) Detachment

Overland detachment coeff (DETACH_ERODE)

Overland detachment exponent (DETACH_EXP)

Overland detachment critical shear (DETACH_CRIT)

10.4.1.2 Overland Sediment Transport Capacity Parameters

GSSHA has several equations that can be used to simulate sediment transport capacity. You can select the appropriate equation for your model based on the information in this manual and in this Sediment Technical Note. You must define and calibrate correct input parameters based on the equation you select with the SOIL_EROSION project card. The following input parameters are used to control the sediment transport equations in each of the six methods:

1 - Engelund-Hansen and 2 - Kilinc Richardson

Overland Transport Capacity Erosion Coefficient (SED_K)

3 - Unit stream power, 4 - Effective stream power, 5 - Slope and unit discharge, and 6 - Shear stress

For the current formulation of these methods, there are no adjustable parameters. Parameters previously assigned by the user, see list of parameters above, are assigned to literature values for the various methods.

10.4.1.3 Sediment Fractions

For each mapping table index, a fraction between 0.0 and 1.0 must be defined for each type of sediment defined in the simulation. The total of these sediment fractions should equal 1.0 so all sediments are included in the particle detachment and sediment transport equations.

10.4.1.4 Overview

Methods for obtaining initial values for the sediment particle detachment parameters and the sediment transport parameters are described in the following sections of this document.

10.4.2 Assignment of Overland Sediment Particle Detachment Parameter Values

The rainfall impact detachment and surface runoff detachment parameters must be initialized to correct values to get reasonable results for the detachment of sediment from the soil surface. For rainfall impact detachment, a rain splash coefficient (SPLASH_K) must be defined. For surface runoff detachment, two parameters--a runoff detachment coefficient (DETACH_ERODE) and a runoff detachment index (DETACH_CRIT) must be defined.

10.4.2.4 Rainfall Impact Detachment Parameter Values

The rain splash coefficient (SPLASH_K) entered in GSSHA is the multiplication of three factors used in Equation 98, which determines rainfall impact detachment. SPLASH_K = (K_I)(C_G)(C_i)

10.4.2.4.1 K_I

K_I is the soil erodibility factor for detachment by raindrop impact. The units for this factor are J^-1 (1/Joules) and the value is approximated using the table 2 from Wicks and Bathurst [1996], shown below:

Soil Texture	Raindrop Erodibility Factor KI, J-1 Meyer and Harmon (1984)	Raindrop Erodibility Factor KI, J-1 Morgan (1985)	Raindrop Erodibility Factor KI, J-1 Bradford et al. (1987 a,b)	Raindrop Erodibility Factor KI, J-1 Verhaegen (1987)
Clay	19.0		73.5
Silty Clay	18.2
Silty Clay Loam	16.2		22.2
Silt	29.8
Silt loam	39.8		25.7	24.7
Loam	28.2	30.0	37.6	23.4
Sandy Loam	32.0		34.4	30.0
Sand			62.4

10.4.2.4.2 C_G

C_G is the ground cover factor and is a value between 0.0 and 1.0. This factor = 1.0 - Fraction of ground covered by ground cover. This factor is unitless and can be obtained from a land use map, a ground cover map, or an aerial photograph.

10.4.2.4.3 C_i

C_i is the cover-management factor and is a value between 0.0 and 1.0. This factor = 1.0 - Fraction of ground covered by canopy cover. This factor is unitless and can be obtained from a land use or a canopy/vegetation cover map or a recent aerial photo of the area being modeled.

10.4.2.5 Surface Runoff Detachment Parameter Values

GSSHA uses three surface runoff detachment parameter values that must be entered in your GSSHA model. The runoff detachment coefficient (DETACH_ERODE, a), the runoff detachment index (DETACH_INDEX, b), and the runoff detachment critical shear (DETACH_CRIT, τ_cr) are used in Equation 101, which determines surface runoff detachment.

10.4.2.5.1 Runoff Detachment Coefficient, a

According to the Water Erosion Prediction Project (WEPP) model documentation, a value of 0.004 for rangeland and a value of 0.05 for cropland should be used for the runoff detachment coefficient.

10.4.2.5.2 Runoff Detachment Index, b

According to the Water Erosion Prediction Project (WEPP) model documentation, a value of 1.0 should be used for the runoff detachment index.

10.4.2.5.3 Runoff Detachment Critical Shear, τ_cr

τ_cr is the runoff detachment critical shear. The units for this factor are Pascals and research is still being conducted on how to obtain this value. We recommend using the default value of 3.5 Pa for this value.

10.4.3 Assignment of Overland Sediment Transport Parameter Values

The Kilinc Richardson and Engelund Hansen transport capacity formulations in GSSHA (Equations 108 and 109) require an erodibility coefficient (SED_K, or K) that varies between zero and unity. As originally formulated for CASC2D, the erodibility factor for the Kilinc Richardson equation contained three factors K, C, and P, that were combined in the equation to describe the overall erodibility of the soil, including the effects of soil texture, vegetation coverage, and management practices. Lower values indicate less erodibility. Although only one factor is currently used in GSSHA, this single factor represents the combined effects of the three original factors contained in the original Kilinc Richardson formulation, as well as other factors. The combined erodibility can thus be assigned based on three original factors as described.

Downer et al (2010) states that the Engelund-Hansen equation is applicable for soils in which <math>\sqrt{D_{75}/D_{25}} < 1.6</math> and for sand-size sediments coarser than 0.15 mm.

The other stream power transport formulations require three parameters that are described in Equation 110 and below.

Downer et al (2010) states that a comparison of the three sediment transport relations in Equations 108, 109, and 110 (Kilinc Richardson, Engelund Hansen, and Stream Power) was performed by running the GSSHA model with each equation. Surprisingly, the result of this comparison showed that for sediments with S=2.65, there is very little difference between them. Therefore, the user is advised to use the Kilinc-Richardson method because it has the smallest number of parameters. However, for simulations involving sediments with specific gravities different from 2.65, the use of the Engelund-Hansen equation is required.

10.4.3.1 Erodibility Coefficient, K

The general erodibility, K, is based on the composition of the soil in each cell. This erodibility can be reduced by vegetative or other coverage with the C factor, and can be further reduced, or increased, by the management practice factor, P. The erodibility coefficient, SED_K = (K)(C)(P).

Soil erosion parameters and soil erosion factors may be estimated from land use, vegetation, and soil texture indices. These values are entered with in the Mapping Table File.

10.4.3.1.1 Soil Erodibility (K)

Soil erodibility describes the susceptibility of the soil to detachment and transport by rainfall impact and overland flow. Soil erodibility is generally a function of soil texture, soil structure, organic content, and permeability. In general, larger particles are harder to erode, as are undisturbed soils. Organic soils are less susceptible to erosion, and have lower K values. The values in Table 17, from Wanielista (1978), are for undisturbed, inorganic soils.

Soil Texture	Erodibility Factor K
Sand	0.05
Loamy sand	0.12
Sandy loam	0.27
Loam	0.38
Silt loam	0.48
Sandy clay loam	0.27
Silt	0.60
Clay loam	0.28
Silty clay loam	0.37

Table 17 – Soil erodibility factor (K) of the modified Kilinc Richardson Equation, Wanielista (1978)

10.4.3.1.2 Cropping Management Factor (C)

The cropping management factor (C) describes the effect of land coverage on reducing the erodibility of bare soils. In general, covered lands are less susceptible to erosion, and have lower C values. With no cover on the soil, the full erodibility (K) can be achieved, and C=1.0. Table 18 lists values for general land coverage types.

Cover	Cropping Factor C
None (fallow)	1.00
Native vegetation	0.01
Crops	0.08
Pasture	0.01
Forest	0.005
Urban	0.01
Other	1.0

Table 18 – Cropping management factors (C), Wanielista (1978) and Goldman et al. (1986)

10.4.3.1.3 Conservation Practice Factor (P)

The conservation practice factor reflects efforts specifically intended to reduce erodibility of the soil. This factor is generally associated with practices used by farmers to conserve the soil, such as no-till and contour farming. This factor may also be important for certain types of construction practices, such as coverage with geotextiles, which tend to reduce erodibility. Other construction practices, such as smoothing and compacting the soil, actually increase erodibility and can result in the value of P being greater than 1.0. Table 19 lists recommended values of P for general land use.

General land use	Control Practice Factor P
Crop	0.5
Pasture	1.0
Forest	1.0
Urban	1.0
Other	1.3

Table 19 – General landuse erosion control factors (P), Wanielista (1978)

10.4.3.2 Stream Power Coefficients, a, b, and ω_c - no longer assigned

The stream power transport formulations require three parameters, a, b, and ω_c, that are described in Equation 110. In this equation, a is a transport coefficient, b is an exponent, and ω_c is a critical stream power. In GSSHA, these are called, respectively, the transport coefficient (TC_COEFF), the transport index (TC_INDEX), and the critical transport capacity (TC_CRIT). In GSSHA version 5.7 and beyond, these parameters no longer assigned by the user. The values are set internally to literature values. These paramters should not be included in the sediment mapping table when using GSSHA versions 5.7 and beyond.

10.4.3.2.1 Transport Coefficient, a - no longer assigned

The Transport Coefficient (TC_COEFF) is used in the stream power equation. No advice is available for determining this parameter from watershed data, so it is recommended that you use Kilinc-Richardson equation (Equation 108) and use the default value of 0.285 for this coefficient.

10.4.3.2.2 Transport Index, b - no longer assigned

The Transport Index (TC_INDEX) is used in the stream power equation. No advice is available for determining this parameter from watershed data, so it is recommended that you use Kilinc-Richardson equation (Equation 108) and use the default value of 1.3 for this coefficient.

10.4.3.2.3 Critical Transport Capacity, ω_c - no longer assigned

The Critical Transport Capacity (TC_CRIT) is used in the stream power equation. No advice is available for determining this parameter from watershed data, so it is recommended that you use Kilinc-Richardson equation (Equation 108) and use the default value of 0.0002 for this coefficient.

10.4.4 Adjusting Overland Elevations during Sediment Simulations=

Unless specified with the ADJUST_ELEV card, changes in elevation due to erosion and deposition are not tracked during the simulation. If the user wishes to include the ongoing effect of erosion and deposition on hydrologic processes during the simulation, the ADJUST_ELEV project card is used to specify this option and to specify the name of a file that will contain the final elevations (in a GRASS ASCII map) at the end of the simulation. The volumetric change in each cell, positive for deposition and negative for erosion can be output using the NET_SED_VOLUME card regardless of whether the ADJUST_ELEV card is used or not so that the user need not include the ADJUST_ELEV card just to get information about the net gain/loss of sediment over the duration of the simulation. The primary purpose of the ADJUST_ELEV card is to include the effects of erosion and deposition on the elevations used during the simulation.

10.4.5 Channel Routing of Sediments

If explicit channel routing is specified in the project file with the CHAN_EXPLIC or DIFFUSIVE_WAVE project cards along with the SOIL_EROSION project card, sediment routing in channels will also be performed. In the CHAN_INPUT file, the user specifies the initial cross-section of each channel link. For each erodible link the maximum depth of erosion is specified with the MAX_EROSION card. Proper construction of a channel input file is given in Section 5 of this manual.

10.4.6 Output

When simulating sediment routing the volumetric flux of sediment at the outlet (cms) is output with the project card OUTLET_SED_FLUX followed with the name of the file for the output. This is a REQUIRED card. The outlet sediment flux will be output at the channel outlet, if channel routing is specified, or at the specified overland flow outlet cell. The format of the outlet sediment flux is a time stamp followed by a column of flux (cms) for each sediment particle specified in the mapping table file. Wash load particles are listed first, in the order specified in the mapping table file, followed by the sand and larger size particles, also in the order specified in the mapping table file. In addition to the specified sand size particles there is one additional column for sand or larger sizes that represents the bed load originally in the channel, so that even if no sand size particles are specified in the mapping table file, the user will still see one column representing bed load for the initial channel sediments. If channel routing is being conducted, then the same information can be output at interior link/node locations using the IN_SED_LOC card, to specify the desired sedograph link node pairs, and the OUT_SED_LOC card which specifies the name of the file that will contain sedographs at the desired locations. The information in the OUT_SED_LOC file will be same as in the OUTLET_SED_FLUX file, except there will be a series of data for each chosen output link/node pair. Data from the link/node pairs in the OUT_SED_LOC file will be listed in the order they were specified in the IN_SED_LOC file. The format of the IN_SED_LOC file is exactly the same as the format for the IN_HYD_LOCATION file, and if the same points are desired for sediment flux as flow, then the same file can be used for both. Additionally, the concentration (mg/L) of total suspended sediments (TSS) at the outlet can be output with the OUTLET_SED_TSS card which is used to specify the file for the outlet TSS information. TSS at interior points can be specfied using the OUT_TSS_LOC card. The link node pairs for the OUT_TSS_LOC file are specified in the file named by the IN_SED_LOC card. Additional information about the output available for sediment processes can be found in Section 3.13.3 of the User's Manual.

Maps of the maximum sediment flux (cms) and the volumetric change (m3) can be output using the MAX_SED_FLUX and NET_SED_VOLUME cards, respectively. Additional information about the output available for sediment processes can be found in Section 3.13.3 of the User's Manual.