Difference between revisions of "Help:Contents"

Latest revision as of 16:42, 23 April 2009

Sediment in Lakes

In GSSHA, three types of sediment lake interaction are taken into account. They are:

1) Sediment entering from overland flow and channel flow to lakes.

When overland routing cell and / or channel routing link’s node encounters a lake, the routed sediment defined in overland erosion and channel sediment transport either settles on the lake covered overland cells or remains in suspension. Basically the sand sized particles, particles having size diameter greater than 0.1 mm are settled on the receiving lake cells. Classes of particle having particle size diameter less than 0.1mm, wash load, either settles in the lake or remains in suspension. The suspended sediment determines the lake sediment concentration and this concentration determines how much sediment is let out of the lake if there is discharge from lake to overland cells or channels.

2) Sediment after entering the lake cells.

-> For each class of particle size, the fall velocity, also referred as terminal velocity or settling velocity, is calculated.

-> The total settled volume of each class particle sized wash load is defined as

    ss_vol_lake_settled[k] = fall_vel[k] * dt* lake_area            

(provided the settled volume does not exceed the vol of that particular sediment size class concentration in the lake.) where, k is the particular class of wash load size, ss_vol_lake_settled[k] is the settled volume of k class of wash load, fall_vel[k] is the terminal velocity of the k class wash load, dt is the routing time step lake_area is the current time lake wetted area.

The settled volume is uniformly distributed among all lake cells.

-> Suspended sediment of each particle size class, ss_vol_lake[k] is defined as

     ss_vol_lake[k]=sed_vol_overland_to_lake[k]  -  ss_vol_lake_settled [k]

where, sed_vol_overland_to_lake[k] is the total volume of each particle size class of wash load entered in the lake from overland and channel at current time step.

->Suspended sediment concentration of each particle size class, ss_conc_vol_lake[k] is defined as

    ss_conc_vol_lake[k] = ss_vol_lake[k] / lake_vol

where lake_vol is the current time lake wetted volume.

Terminal velocity derivation Terminal velocity in the presence of buoyancy force: When the buoyancy effects are taken into account, an object falling through a fluid under its own weight can reach a terminal velocity (settling velocity) if the net force acting on the object becomes zero. When the terminal velocity is reached the weight of the object is exactly balanced by the upward buoyancy force and drag force. That is

W=Fb+d .............. 1

where W = weight of the object, Fb = buoyancy force acting on the object, and D = drag force acting on the object. If the falling object is spherical in shape, the expression for the three forces is given below:

W = π/6*d^3*ρs*g .............. 2

Fb = π/6*d^3*ρ*g ............... 3

D = Cd*1/2*ρ*V^2*A ............... 4

where d = diameter of the spherical object g = gravitational acceleration, ρ = density of the fluid, ρs = density of the object, A = πd2 / 4 = projected area of the sphere, Cd = drag coefficient, and V = characteristic velocity (taken as terminal velocity, Vt). Substitution of equations (2–4) in equation (1) and solving for terminal velocity, Vt to yield the following expression

Vt = sqrt(4*g*d/3/Cd*(ρs-ρ)/ρ) ............. 5

Terminal velocity in creeping flow

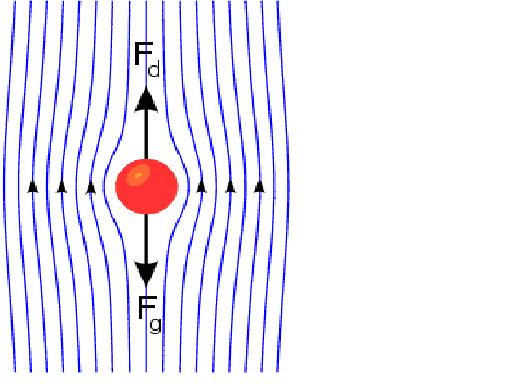
Fig. Creeping flow past a sphere: stream lines, drag force Fd and force by gravity Fg.

For very slow motion of the fluid, the inertia forces of the fluid are negligible (assumption of massless fluid) in comparison to other forces. Such flows are called creeping flows and the condition to be satisfied for the flow to be creeping flows is the Reynolds number . The equation of motion for creeping flow (simplified Navier-Stokes equation) is given by

▼p = μ▼^2v .................... 6

where v= velocity vector field p = pressure field μ = fluid viscosity The analytical solution for the creeping flow around a sphere was first given by Stokes in 1851. From Stokes' solution, the drag force acting on the sphere can be obtained as

D = 3*π*μ*dV or Cd = 24/Re ....7

where the Reynold's number, Re = ρdv/μ. The expression for the drag force given by equation (7) is called Stokes law. When the value of Cd is substituted in the equation (5), we obtain the expression for terminal velocity of a spherical object moving under creeping flow conditions:

Vt = g*d^2/18/μ*(ρs-ρ) ....................8

Equation 8 is used in GSSHA to derive the fall velocity of the sediment in the lakes. Other Applications: The creeping flow results can be applied in order to study the settling of sediment particles near the ocean bottom and the fall of moisture drops in the atmosphere.

3) Wash load leaving from Lake Cell to overland flow and channel.

If discharge is from the lake cell to the over land receiving cell or towards the channel, suspended sediment volume of each particle size class discharged by the lake’s out go cell is defined as

   vol_sed_discharged = ss_conc_vol_lake[k] * q *dt

where, ss_conc_vol_lake[k] is the suspended sediment concentration of k particle size class, q is the water discharge from the lake and dt is the routing time step.