Alternate Run Modes:Automated Calibration with Shuffled Complex Evolution

Calibration Mode

The automated calibration method is intended to both ease the burden of manual calibration and to increase the users ability to explore the parameter space and search for the optimal solution as defined by the user. GSSHA™ employs the Shuffled Complex Evolution method (SCE) (Duan et al., 1992). The SCE method was originally coded in FORTRAN as a stand-alone program using text files to communicate with other models but was recoded by Fred Ogden and Aaron Byrd into C++ as a class that can wrap around any functional model and incorporated into the GSSHA™ source code.

The SCE method uses the result of a cost function to assess the progress of the calibration. The cost is a numerical value that indicates goodness of fit of a simulation to a observed data set. As of the date of this update to the wiki, the automated calibration method contained within GSSHA™ can be used to calibrate parameters for discharge and for sediments. Calibration to outlet discharge can be performed for overland flow and channel discharge. For sediments, automated calibration can only be used for channel sediment discharge. Sediment parameters are calibrated to the wash load, or fines, which is represented by values of Total Suspended Solids (TSS). Calibration to internal points can only be done for channel discharge. The cost is derived from a comparison of storm event peak discharges and volumes between measured and observed. For sediments, peak sediment discharge and event sediment discharge volume are used. Calibration is typically conducted for long term simulations with multiple events, but calibrations to a single event can also be performed.

The absolute difference between observed and simulated for each storm event peak discharge and volume is calculated and then normalized by dividing the absolute error by the observed peak discharge or storm volume. This results in errors being specified as fractions of the observed values. The user specifies the importance of each observation with weighting factors that are applied to each of the observed values. The cost is the sum of the errors multiplied by the weighting factors. The SCE method will attempt to minimize this cost by varying parameter values within a range specfied by the user in the SCE control file. The definition of the cost will play a large role in the final set of parameter values derived by the SCE process. For the SCE method as incorporated into GSSHA™, the weights placed on each event peak discharge and volume determine how the cost function is calculated. Thus, the weights specified by the user have a significant effect on the final set of parameter values, and the resulting parameter values may change dramatically as the weights are modified. Therefore, if the calibration converges on results deemed inadequate for the purposes of the study, different results may be obtained by changing the weights and repeating the calibration. Additional details on the method can be found in Senarath et al. (2000).

The SCE method is very good at finding the absolute minimum cost while avoiding becoming trapped in local minima. However, the methods employed result in numerous simulations being required. Depending on the number of parameters to be calibrated, the paramater ranges, and the required convergence criteria the method will require hundreds to thousands of simulations to converge on a solution. Somewhere between 500 and 5,000 simulations are typically required. More simulations are required for more parameters, for larger parameter ranges, and for smaller convergence criteria. For this reason, the number of calibration parameters should be minimized, with only the most sensitive paramters being calibrated.

To utilize the SCE method for calibration in GSSHA™, GSSHA™ is run in the calibration mode by typing the following on the command line

gssha –c calib_file.in

where calib_file.in is the name of the calibration control file.

The calibration control file, as described below, contains all of the information needed to control the SCE simulation. In should be noted that for automated calibration the REPLACE_PARAMS and REPLACE_VALS cards are NOT used in the GSSHA™ project file.

Calibration Input File

The SCE control file contains the file names for the project file (Section 3), the parameter list (Section 18.2), and the observed data file (described below), followed by the control parameters, and then a list of initial, minimum and maximum values for the parameter list. The SCE method will search the parameter space for the supplied parameter list within the range of values specified under the conditions described in the control parameters until the method converges on a solution or until the maximum number of simulations is exceeded. The calibration file contains the following information in the format displayed below:

Projname.prj
Params.in
Observed.dat
[maxn]	[kstop]	[pcto]	[ngs]	[iseed]	[use_defaults]	[No. params]
[npg]	[nps]	[nspl]	[mings]	[iniflg]	[iprint]	
[init val]	[low val]	[high val]
[init val]	[low val]	[high val]
…
[init val]	[low val]	[high val]

Where: in line 1

Projname.prj is the project file name

Params.in is the parameters file name (described in section 18.?)

Observed.dat is the observed data file name (described below)

Maxn =maximum number of simulations

Kstop = stop if after the last x simulations no change greater than Pcto has occurred

Pcto = percent change in cost function that must occur for the simulation to continue

ngs = number of complexes in the initial population

Iseed = random number seed

Use_defaults = use internal default values for the values on the second line

= 0, use defaults

= 1, use values on second line

No. params = number of parameters to vary

And in line 2

npg = number of points in each complex (default is 2*(No. params)+1)

nps = number of points in a sub-complex (default is No. params +1)

nspl = number of evolution steps allowed for each complex before complex shuffling (default is npg)

mings = minimum number of complexes required, if the number of complexes is allowed to reduce as the optimization proceeds (default is ngs)

iniflg = flag on whether to include the initial point in population

= 0, not included (default)

= 1, included

iprint = flag for controlling print-out after each shuffling loop

= 0, print information on the best point of the population (default)

= 1, print information on every point of the population

Followed by one line for each calibration parameter:

Init_val is the initial value of the parameter

Low_val is the lowest possible value of the parameter

High_val is the highest possible value of the parameter.

An example file is shown below.

inf_calib1.prj						
params1.in						
observed.dat						
1000	5	1	4	2986	1	1
3	2	3	3	0	0	
0.5	0.010	2.0

This calibration file for one parameter, allows up to 1000 simulations, and specifies that the best result must change by 1% or more in five simulations (kstop) to keep going. A random seed (Iseed) of 2986 is used to initialize the random number generator, and there are 4 complexes (ngs) in the initial population. The initial parameter value is 0.5 and the parameter will be allowed to vary between 0.01 and 2.0. Default values (generated from the number of complexes and number of parameters) will be used for the other control values.

Observed Data File

The observed data file describes the peak discharge and discharge volume for each event, as well as a weighting for each peak and volume. Unless you use the QOUT_CFS flag, make sure that peak discharges are in m³s^-1 and event volumes are m³. If you use the QOUT_CFS flag in your project file make sure that peak discharges are in ft³s^-1 and event volumes are in ft³.

The following format is used:

[# of events]
[Event #1 Peak]  [Weight on Peak 1]  [Event #1 Volume]  [Weight on Vol 1]
[Event #2 Peak]	 [Weight on Peak 2]  [Event #2 Volume]  [Weight on Vol 2]
[Event #3 Peak]	 [Weight on Peak 3]  [Event #3 Volume]  [Weight on Vol 3]
…
[Event #N Peak]	 [Weight on Peak N]  [Event #N Volume]  [Weight on Vol N]

The events must correspond to the events in the precipitation file, and the volume calculations should end once the EVENT_MIN_Q flow rate (user specified in the project file) is reached in the observed data. The event start and end times can be found in the SUMMARY file. The weights can be any postive real number but for the easiest to interpret results all of the weights should add up to 1.0. If all the weights sum to one then the cost function results can be interpreted as the mean absolute error.

For example, the observed file

5
0.0  0.0    0.0 0.0
2.4  0.0   53.3 0.0
16.5 0.25 103.4 0.25
0.0  0.0    0.0 0.0
8.3  0.25  75.2 0.25

contains information for five events, but only two will be used for calibration. For this example the first event that produces runoff is given a weight of zero and the other two event peaks and volumes are equally weighted.

Because of the uncertainty in defining initial moistures the typical approach is to not use the first large event for calibration but to instead use that event and the subsequent period after the event to initialize the soil moistures for the next event. Senarath et al. (1995) demonstrated that the importance of the value of the initial moisture estimation diminishes significantly after the first rainfall event.

Altough the weights are equally distributed between peaks and volumes for this example, the weight on the peaks and volumes can be different. Senarath et al. (2000) suggests weighting peaks and volumes equally or near equally, with no more than 70% of the emphasis on either the peak or the volume.

The weighting can also vary from storm to storm. Since very small events are typically subject to large errors in measurement, are difficult to reproduce, and are not usually important in terms of flooding, total discharge, or sediment and contaminant transport, they are typically weighted very little, if at all (Ogden et al., 2001). Emphasis is usually placed on larger events, or events of the magnitude relevant to the problem at hand.

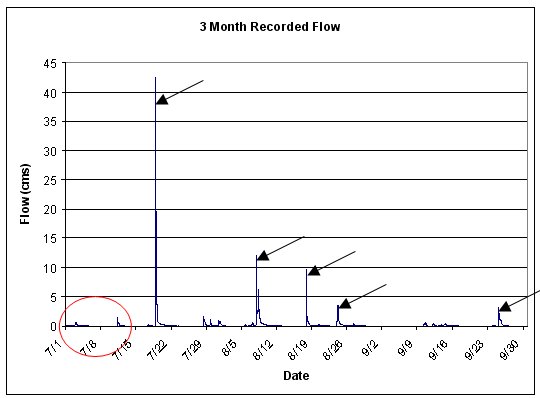
For the example data depicted in the figure below, the weighting on the first two small events should be zero or minimal, with the majority of the weight placed on the following large events. A good rule of thumb is to weight events in proportion to the magnitude of the discharge from the event. To allow the model to properly initialize the the soil moistures, the weight on the first large event occuring around July 22 should also be zero.

If internal measurements are available in the watershed they can also be incorporated into the calibration. Multiple measurement points result in more robust calibrations. Multiple gages can only be used when simulating channel flow. For calibrating to multiple gages include the observed discharge locations in the input hydrograph location file, and then include those data in the observed data file on individual lines after each set of outlet data for each event. For example, if there are four internal gages the observed data file should have the following format. For four gages and three events, the number of records would be 15. The internal locations are specified in the IN_HYD_LOCATION file. The values in this file must correspond to the number and order of gages specified in the IN_HYD_LOCATION file. You must include a line for every link/node pair in the IN_HYD_LOCATION file, even if the weight is zero.

[# of records]
[Event #1 (outlet) Peak]  [Peak Weight]	[Event #1 (outlet) Volume]  [Volume Weight]
[Event #1 (ihl#1) Peak]   [Peak Weight]	[Event #1 (ihl#1) Volume]   [Volume Weight]
[Event #1 (ihl#2) Peak]   [Peak Weight]	[Event #1 (ihl#2) Volume]   [Volume Weight]
[Event #1 (ihl#3) Peak]   [Peak Weight]	[Event #1 (ihl#3) Volume]   [Volume Weight]
[Event #1 (ihl#4) Peak]   [Peak Weight]	[Event #1 (ihl#4) Volume]   [Volume Weight]
[Event #2 (outlet) Peak]  [Peak Weight]	[Event #2 (outlet) Volume]  [Volume Weight]
[Event #2 (ihl#1) Peak]   [Peak Weight]	[Event #2 (ihl#1) Volume]   [Volume Weight]
[Event #2 (ihl#2) Peak]   [Peak Weight]	[Event #2 (ihl#2) Volume]   [Volume Weight]
[Event #2 (ihl#3) Peak]   [Peak Weight]	[Event #2 (ihl#3) Volume]   [Volume Weight]
[Event #2 (ihl#4) Peak]   [Peak Weight]	[Event #2 (ihl#4) Volume]   [Volume Weight]
…
[Event #N (outlet) Peak]  [Peak Weight]	[Event #N (outlet) Volume]  [Volume Weight]
[Event #N (ihl#1) Peak]   [Peak Weight]	[Event #N (ihl#1) Volume]   [Volume Weight]
[Event #N (ihl#2) Peak]   [Peak Weight]	[Event #N (ihl#2) Volume]   [Volume Weight]
[Event #N (ihl#3) Peak]   [Peak Weight]	[Event #N (ihl#3) Volume]   [Volume Weight]
[Event #N (ihl#4) Peak]   [Peak Weight]	[Event #N (ihl#4) Volume]   [Volume Weight]

Project File

There are no specific project cards required for use with the SCE method. The required control parameters are contained in the SCE control file, as described above. The REPLACE_PARAMS and REPLACE_VALS cards described in Section 18.2 should NOT be used. The METRIC card should be specified in the project file. If the QOUT_CFS card is used make sure your observed values are in English units. In order to speed up the automated calibration process only required output files should be generated. In particular, make sure not to produce any time series maps. Use the QUIET or SUPER_QUIET card to suppress printing output to the screen. If you want to use sediment data to optimize sediment parameters include the OPTIMIZE_SED card in the project file.

Output Files

GSSHA produces multiple additional output files when run in the automated calibration mode. A brief description of the most useful files for users is presented below.

Best.out - contains a list of the final parameter values determined by the calibration.

sce_output.out - contains the detailed output from the SCE model including start up information and warnings, information from each suffling loop, as well as the final results.

log_file.txt - the log file list the cost, the minimum cost for the simulation, and the associated parameter values for each simulation. The log_file.txt file can be used to track the progress of the calibration. In case of power failure or a system crash during the calibration, the best value from the log_file.txt file can be used as the initial value in the SCE control file for a repeated simulation.

Forward Run

To see the results of the calibration you need to use the parameter set determined by the calibration to simulate the calibration period. This is called the forward run. The simplist way to produce the forward run is to make a simulation with your calibration input files using the replacement method (Section 18.2). As described above, the best parameter set can be found in the "best.out" file. Use these parameter values to make the REPLACE_VALS file. The REPLACE_PARAMS file already exist from your calibration. With these minor changes to your project file complete, run the project file in normal GSSHA mode, not in calibration mode, to see the simulation results with the optimized parameter set.

Calibration of Sediment Parameters

You can calibrate to sediment output in exactly the same manner as with flow. Everything is the same except in the project file you must include the card OPTIMIZE_SED and in the observed data file you must substitute the sediment discharge, peak discharge m³s^-1 and event volume m³. The observed data should be the wash load (fines smaller than the specified size of sand, ie silt and clay). To optimize the sediments you must be working in metric units. In general, the only sediment parameter that is calibrated is the overland flow erodibility factor, SED_K. In certain circumstances including the rainfall detachment coefficient SPLASH_K, may improve the calibration results. Suggested starting parameters values for sediment simulations are given in Chapter 10 of the manual.

Summary of Automated Calibration Mode

1. Calibrations are based on comparisons to event peak discharge and discharge volume.
2. The importance of each event peak and volume is determined by the weight assigned
to that measurement.
3. Calibrations are best performed in the continuous mode for a period of record that
includes multiple events of various sizes, including events similar to the ones of
interest.
4. The first large event should be used for system initialization, and assigned a
weight of zero.
5. Weights for subsequent observations should be proportional to the value of the
observation.
6. To simplify interpretation of results, all weights should sum to 1.0.
7. Internal gages can be used if channel routing is being performed.
8. Use of internal gages increases robustness of the calibration.
9. Automated calibrations require hundreds to thousands of simulations.
10. To reduce simulation time minimize the number of parameters being calibrated.
11. Perform a sensitivity study to determine the important parameters for calibration.
12. Suppress printing output to the screen and to files.
13. If the final parameter values are at or near the maximum or mimimum values
consider relaxing the the values and repeating the calibration.
14. If the final parameter values do not produce the desired results modify the
weights on the observations.
15. Always use the best values from the previous calibration as the initial values for
subsequent calibration attempts.
16. To see model results with the calibrated parameters , make a forward run using the
values in the "best.out" file while running your project with value replacement.
17. GSSHA can be calibrated to sediment data by including the '''OPTIMIZE_SED''' card in
the project file and using the observed sediment data in the observed data file.
18. Sediment calibrations are based on the wash load, fines smaller than the user specified
sand size.