Continuous:Computation of Evaporation and Evapo-transpiration
The evaporation and evapo-transpiration models incorporated in GSSHA allow calculation of the loss of soil water to the atmosphere, improving the determination of soil moistures. Two different evapo-transpiration options are included:
- bare-ground evaporation from the land-surface using the formulation suggested by Deardorff (1978), and
- evapo-transpiration from a vegetated land-surface utilizing the Penman-Monteith equation (Monteith, 1965, 1981).
Variants of these two representations are widely used in land-surface schemes of climate and distributed hydrologic models (e.g., Dickinson et al., 1986; Beven, 1979).
To accurately compute fluxes of soil water to the atmosphere, energy fluxes between the atmosphere and the ground must first be computed. These energy, or radiation, fluxes, discussed in Section 9.1.1, are the forcing terms in the evapo-transpiration calculations. Ground temperature is an important component in both the Deardorff and Penman-Monteith formulations, and the fluxes computed in Section 9.1.1 are used in the computation of the ground temperature as described in Section 9.1.2. A detailed presentation of the Deardorff method in Section 9.1.3 describes how the computed fluxes and ground temperatures can be related to bare-soil evaporation. Section 9.1.4 details how the computed fluxes are adjusted and applied for computation of evapo-transpiration with the Penman-Monteith equation. Finally, Section 9.1.5 describes the additional inputs needed for ET calculations.
9.1.1 Computation of Auxiliary Energy and Heat Fluxes
Realistic estimates of incoming and outgoing radiation fluxes are needed for accurate estimates of ET. The important components of the energy budget are long-wave radiation, discussed in Section 9.1.1.1, short wave radiation, discussed in Section 9.1.1.2, and heat conduction into the soil, Section 9.1.1.3. Influences of soil, water, vegetation and cloud albedos, atmospheric emissivities, and sloping-terrain effects on energy fluxes must be included in the calculations. The effects of albedos and emissivities are of great importance in determining radiation fluxes and warrant detailed representation (Pielke, 1984).
9.1.1.1 Net Incoming Short-wave Radiation
The net incoming short-wave radiation can be represented as:
where: A is the albedo, and Rs, direct and Rs, diffuse are direct and diffuse contributions of short-wave radiation, respectively.
It is also imperative that short-wave energy influxes be modified to account for sloping terrain effects. As described by Young (1972), even in the Great Plains region of North America (one of the flattest places on earth), only 7% of the land area can be classified as flat in relation to solar radiation calculations. Despite the significance of terrain, most hydrologic and Global Climate Model (GCM) land-surface schemes ignore the sloping terrain effects when estimating the soil energy budgets. Pielke (1984) found substantial differences between the solar radiation values from north and south facing slopes. Pielke and Mehring (1977) found that “the eastern slope of a 1-km mountain (with a slope of about 2°) to be about 1° to 2°C warmer in the morning and cooler by the same amount in the afternoon than the same location in the western slope.” The direct incoming solar irradiance can be represented as:
where: λ is angle of incoming radiation, ζ is the local land surface slope in the azimuthal direction of the sun, and Rs, horiz,direct,ground is the direct radiation on a horizontal ground surface, computed as:
where: the transmission coefficient, Kt (dimensionless) is a function of density, type and condition of vegetation, N is the fraction of sky covered by cloud cover (0-1), n is a turbidity factor of air that varies from 2.0 (clear air) to 5.0 (smoggy urban areas), currently fixed at a value of 2.0 in the code. K is the fraction of cloudless sky insolation received on a day with overcast skies, and is given as:
where z is the height to the cloud-base (km), fixed in the current formulation at 1.5 km. The molecular scattering coefficient, a, is defined as:
The optical air mass, m, is calculated as:
where: λ is the angle from the observer’s horizon to the center of the solar disk, and is often referred to as the “solar elevation angle”. Calculation of λ is discussed below.
If no measurements of Rs,horz,direct are available, then they may be estimated based on the time of day and year, and the location of the watershed from:
|
|
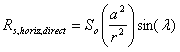 , if λ < 90°, and , if λ < 90°, and |
(59a) | |
|
|
|
(59b) |
where the solar constant, So, has a value of 1376 W m-2 (Hickey et al., 1980). Following Paltridge and Platt (1976) the ratio of the actual earth-sun distance squared (a2) to the average earth-sun distance squared (r2) on any given Julian day m* can be estimated using the following relationship (60):
where:
where: m* is the number of the day [i.e., ranging from 0 (January 1) to 364 (December 31)], and do is the Julian day fraction of the year converted to radians. The angle (i) between the direct solar radiation and the normal to the slope is defined as (Kondrat’yev, 1969) :
The slope of the terrain (α) is given by:
where: ∂zG/∂x and ∂zG/∂y represent the incremental slopes in the x and y directions. The zenith angle (λ) is defined by:
where: angle φ is the latitude at the site of interest. The orientation of the sun’s azimuth β relative to the azimuth of the terrain slope γ is given by β–γ. The trigonometric relationship for γ is:
The trigonometric relationship for β is:
where: δsun is the declination angle of the sun (varying between +23.5? on June 21 to -23.5? on December 22), and can be obtained by using the following formulation (Paltridge and Platt, 1976):
where: δsun is in radians. The hour angle, hr (0°≡noon) is represented mathematically when the sun is east of the observer’s longitude as follows (Curtis and Eagleson, 1982):
where: Ts is the standard time at the site of interest (counted from midnight; i.e. from 0.00 to 23.59), ΔT2 is the difference between true solar time and mean solar time in hours (small; hence is neglected in this analysis), and ΔT1 is the difference between the standard and local longitudes (in hours) given as:
where i* = 1 for longitudes located to the east of Greenwich and i* = -1 for those located to the west, and θS and θL are the longitudes of the standard- and the observer-meridian, respectively. The standard-meridian is defined as the meridian where the observer’s time zone is centered. When the sun is west of the observer’s longitude the following relationship is used:
The diffuse short-wave radiation is obtained by using the following relationship (Kondrat’yev, 1965):
Lee (1978) noted that the difference between Rs,diffuse and Rs,horiz.,diffuse is only 2% for slopes less than 30%. Lee (1978) also showed that for slopes less than 36%, the contribution to the total solar radiation by the reflection of total solar from surrounding sloped terrain is only 3% or less. The diffuse horizontal radiation, Rs,horiz.,diffuse data are extracted from NOAA-NREL CD-ROMs, and hence atmospheric scattering and absorption effects are neglected.
9.1.1.2 Net Incoming Long-wave Radiation
The net incoming long-wave radiation can be represented as follows:
where: A is the long-wave surface albedo, σ is the Stephan-Boltzmann constant with a value of 5.67 x 10-8 Jm-2s-1K-4, Tg and Ta are the absolute ground and the air temperatures (Kelvins), respectively, K* is the cloudiness-correction factor (dimensionless), and Ea and Eg are the emissivities of the air and the ground surfaces, respectively (dimensionless). Following Bras (1990), it is assumed that the ground surface acts as a blackbody, with an emissivity of 1.0. The long-wave radiation from clear skies is strongly related to the atmospheric water content. The following formulation is used to evaluate the atmospheric emissivity (Idso, 1981):
where e is the vapor pressure (mb), and can be obtained from the following relationship:
where: rh is the relative humidity (dimensionless, expressed as a decimal number between 0 and 1), and es is the saturated vapor pressure (mb). Using the Teten’s formula (Teten, 1930) the saturated vapor pressure can be approximately evaluated as:
The presence of clouds gives rise to an increase in long-wave radiation. The following relationship, suggested by the TVA (1972), is used to evaluate K*:
where N is the fraction of sky covered by clouds.
9.1.1.3 Heat Conduction into the Soil
Many models neglect the soil heat flux (Manabe et al., 1974; Gates, 1974), however, Deardorff (1978) has found the assumption of an insulated soil surface to be especially poor under random atmospheric forcing-conditions. Following Kasahara and Washington (1971), in GSSHA the soil heat flux at the surface (positive when directed into the soil) is represented as a function of sensible heat flux. Deardorff (1978) found the following relationship to be of “intermediate but surprisingly acceptable accuracy” in determining the sum of energy fluxes into the soil (W m-2) for short time-steps:
where Hs is the sensible heat flux (W/m2) (positive when directed upward), represented mathematically as:
where: cp is the specific heat at constant pressure, equal to 1.013 kJ kg-1 °C-1, ua is the wind speed (m/s) at the reference level, z, and cH is the dimensionless heat or moisture transfer coefficient applicable to bare soil. Following Deardorff (1978) a value of 0.0025 is selected for cH. The air density ρa is calculated as (kg m3):
where: Pa is the atmospheric pressure in kPa, and Ta is the air temperature in °C.
9.1.2 Estimation of Ground Temperature
Because ground temperature appears explicitly in the outgoing long-wave energy flux-term, and implicitly in the Deardorff (1978) and Penman-Monteith evaporation formulae, it is important for radiation and evaporation calculations. Ground temperature varies considerably during the diurnal cycle and is not generally measured or provided by meteorological or weather stations. In GSSHA the ground temperature is obtained numerically by solving the surface energy balance equation with the Newton-Raphson iterative method as described by Deardorff (1978).
Assuming that the energy lost due to temporary storage, advection and biochemical usage are negligible for non-vegetated surfaces, the surface energy balance formulation can be written as:
where: the terms Hs, Rl, Rs and G have been previously defined, and E is the evaporation latent heat flux (W/m2) from bare soil, as described in Section 9.1.3.
The saturation specific humidity (kg/kg), a function of ground temperature, qsat (Tg) (mb) can be calculated from:
where: ε is the ratio of molecular weight of water vapor to that for dry air (0.622), and qa is the specific humidity, estimated by substituting e = rhes for es, where rh is the relative humidity.
The Clausius-Clapeyron equation is used to calculate the derivative of qs with respect to Tg as:
where: Rwater is the gas constant for water vapor (461 J kg-1 °K-1) and L is the latent heat of evaporation (2.50036 MJ kg-1). Following Williamson et al. (1987), the latent heat of evaporation, known to vary with ground temperature, is a constant. The ground temperature can be obtained iteratively using the following relationship:
where: K indicates the iteration count, ƒ(Tg) is obtained from Equation (80) and ƒ’ (Tg) is obtained from Equation (82). The initial value for the iterative procedure is the surface temperature from the previous time step, Tgn-1. The procedure is repeated until the following condition is satisfied:
A convergence criterion, δe of 0.001 °K is utilized in this analysis. When the convergence criterion is satisfied the Clausius-Clapeyron equation is solved, and Tgn = Tgk+1.
9.1.3 Evapo-transpiration
Evaporation from a bare surface can be computed using the Deardorff equation by specifying the ET_CALC_DEARDORFF card in the project file. When using the Deardorff method only the physical components of evaporation are considered. Plants are not considered. Compared to the Penman-Montieth method (1971), use of the Deardorff method can result in higher evaporation and lower soil moistures because residual soil moisture is the lower limit on soil moisture and resistance of the plant canopy to evaporation is not considered. The Deardorff method is not appropriate in vegetated areas and have limited applicability. Inputs to the mapping table for ET calculations, described below, are the same for the two methods.
The ET_CALC_PENMAN project card is used to select the Penman-Monteith method for evapo-transpiration. The Penman-Monteith equation is one of the most advanced resistance-based models available for the prediction of evapo-transpiration from a vegetated land-surface (Shuttleworth, 1993). Although Monteith (1965) points out several simplifying assumptions utilized to derive the Penman-Monteith evaporation formula, Lemeur and Zhang (1990) have found that for arid watershed the performance of the Penman-Monteith is better than both the CRAE (Morton, 1983) and the Advection-Aridity (Brutsaert and Stricker, 1979) models. In the Penman-Monteith model, the potential evapo-transpiration estimates are obtained by using the following relationship:
where:
- Δ is the slope of the specific humidity/temperature curve between the air temperature and the surface temperature of the vegetation (kPa °C-1)
- λ is the latent heat of vaporization of water (2.50036 MJ/kg)
- cp is the specific heat of air at constant pressure (1.013 kJ kg-1 °C-1)
- γ is the psychrometric constant kPa °C-1)
- ra is the aerodynamic resistance to the transport of water vapor from the surface to the reference level z (s/m)
- rc is the (Monteith) canopy resistance (s/m) to the transport of water from some region within or below the evaporating surface to the surface itself. The canopy resistance is expected to be a function of the stomatal resistance of individual leaves. Under wet-canopy conditions rc = 0.
- A* is the available energy given by A* = (Rl + Rs) - G (W/m2)
- Rs is the net incoming short-wave radiation at the reference level z, (W/m2) Section 9.1.1.1.
- Rl is the net long-wave radiation at the reference level z, (W/m2) Section 9.1.1.2.
- G denotes the sum of energy fluxes into the ground, to adsorption by photosynthesis and respiration and to storage between ground level and z (in W/m2), Section 9.1.1.3.
The standard reference level, z, is taken as 2 m. The current formulation does not explicitly calculate the leaf temperature of the vegetation canopy, and the ground temperature is substituted for the leaf temperature when calculating Δ. The psychrometric constant, γ, is defined as:
where: P is the atmospheric pressure (kPa). The gradient of the saturation vapor pressure curve with respect to temperature, Δ, is given by:
The rate of water diffusion from the ground surface due to turbulence is controlled by the aerodynamic resistance term, ra. This term is a function of wind speed and the height of the vegetation cover. Mathematically, ra is represented as:
where: zu and ze are the heights of the wind speed and humidity measurements (m), respectively, and Uz is the wind speed (m/s). Following Brutsaert (1975), zom is assumed to be 0.123hc and zov is assumed to equal 0.0123hc, where hc is the mean height of the crop (m). According to Monteith (1981) d = 0.67 hc.
9.1.4 Parameter Values
Calculation of evapo-transpiration requires additional parameter values be assigned to every active grid cell. These parameters may be assigned with either the Mapping Table File, Section 11, or GRASS ASCII maps specified with project cards described in Section 3.8. ET parameters are typically assigned with a combination soil texture/land use (STLU) index map. The Deardorff method requires values of land surface albedo. For the Penman-Monteith method, values of land surface albedo, vegetation height, vegetation canopy resistance, and vegetation transmission coefficient are needed.
9.1.4.1 Land Surface Albedo
Ground surface temperature calculations, discussed in Section 9.1.2, require values of land surface albedo, which describe the fraction of long-wave radiation reflected back to the atmosphere. Values range from 0.0 to 1.0. Literature values for a variety of land covers compiled from a number of sources are listed in Table 11.
| Ground Cover | Albedo |
|---|---|
| Fresh Snow | 0.75 - 0.95b, 0.70 - 0.95c, 0.80 - 0.95d, 0.95e |
| Fresh snow (low density) | 0.85f |
| Fresh snow (high density) | 0.65f |
| Fresh dry snow | 0.80 - 0.95g |
| Pure white snow | 0.60 - 0.70g |
| Polluted snow | 0.40 - 0.50g |
| Snow several days old | 0.40 - 0.70b, 0.70c, 0.42 - 0.70d, 0.40e |
| Clean old snow | 0.55f |
| Dirty old snow | 0.45f |
| Clean glacier ice | 0.35f |
| Dirty glacier ice | 0.25f |
| Glacier | 0.20 - 0.40e |
| Dark soil | 0.05 - 0.15b, 0.05 - 0.15g |
| Dry clay or gray soil | 0.20 - 0.35b, 0.20 - 0.35g |
| Dark organic soils | 0.10f |
| Dry black soil | 0.14i |
| Moist black soil | 0.08i |
| Dry gray soils | 0.25 - 0.30i |
| Moist gray soils | 0.10 - 0.20g, 0.10 - 0.12i |
| Dry blue loam | 0.23i |
| Moist blue loam | 0.16i |
| Desert loam | 0.29 - 0.31i |
| Clay | 0.20f |
| Dry clay soils | 0.20 - 0.35d |
| Dry light sand | 0.25 - 0.45b |
| Dry, light sandy soils | 0.25 - 0.45g |
| Dry, sandy soils | 0.25 - 0.45a |
| Light sandy soils | 0.35f |
| Dry sand dune | 0.35 - 0.45b, 0.37c |
| Wet sand dune | 0.20 - 0.30b, 0.24c |
| Dry light sand, high sun | 0.35f |
| Dry light sand, low sun | 0.60f |
| Wet gray sand | 0.10f |
| Dry gray sand | 0.20f |
| Wet white sand | 0.25f |
| Dry gray sand | 0.35f |
| Yellow sand | 0.35i |
| White sand | 0.34 - 0.40i |
| River sand | 0.43i |
| Bright, fine sand | 0.37i |
| Rock | 0.12 - 0.15i |
| Peat soils | 0.05 - 0.15d |
| Dry black coal spoil, high sun | 0.05f |
| Dry concrete | 0.17 - 0.27b, 0.10 - 0.35e |
| Road black top | 0.05 - 0.10b |
| Asphalt | 0.05 - 0.20e |
| Tar and gravel | 0.08 - 0.18e |
| Densely urbanized areas | 0.15 - 0.25i |
| Urban area | 0.10 - 0.27 with an average of 0.15e |
| Long grass (1 | 0 m) 0.16e |
| Short grass (2 cm) | 0.26e |
| Wet dead grass | 0.20f |
| Dry dead grass | 0.30f |
| High, dense grass | 0.18 - 0.20i |
| Green grass | 0.26i |
| Grass dried in sun | 0.19i |
| Typical fields | 0.20f |
| Dry steppe | 0.25f, 0.20 - 0.30g |
| Tundra and heather | 0.15f |
| Tundra | 0.18 - 0.25e, 0.15 - 0.20g |
| Heather | 0.10i |
| Meadows | 0.15 - 0.25g |
| Cereal and tobacco crops | 0.25f |
| Cotton, potatoes and tomato crops | 0.20f |
| Cotton | 0.20 - 0.22i |
| Cotton plantations | 0.20 - 0.25g |
| Potatoes | 0.19i |
| Potato plantations | 0.15 - 0.25g |
| Lettuce | 0.22i |
| Beets | 0.18i |
| Sugar Cane | 0.15f |
| Orchards | 0.15 - 0.20e |
| Agricultural crops | 0.18 - 0.25e, 0.20 - 0.30d |
| Rice field | 0.12i |
| Rye and wheat fields | 0.10 - 0.25g |
| Spring wheat | 0.10 - 0.25i |
| Winter wheat | 0.16 - 0.23i |
| Winter rye | 0.18 - 0.23i |
| Deciduous forests - bare of leaves | 0.15e |
| Deciduous forests - leaved | 0.20e |
| Deciduous forests | 0.15 - 0.20g |
| Deciduous forests - bare with snow on the ground | 0.20d |
| Mixed hardwoods in leaf | 0.18f |
| Rain forest | 0.15f |
| Eucalyptus | 0.20f |
| Forest - pine, fir, oak | 0.10 - 0.18c |
| Forest - coniferous forests | 0.10 - 0.15g, 0.10 - 0.15d |
| Forest - red pine forests | 0.10f |
| Tops of oak | 0.18i |
| Tops of pine | 0.14i |
| Tops of fir | 0.10i |
| Water | 0.0139 + 0.0467 tan Z, 1 >= A >= 0.03h |
Table 11 – Land surface albedo values Notes: aThe smaller value is for high zenith angles; the larger value is for low zenith angles. From bSellers (1965); cMunn (1966); dRosenburg (1974); eOke (1973); fLee (1978); gde Jong (1973); hAtwater and Ball (1981); and iEagleson (1970).
9.1.4.2 Canopy Stomatal Resistance
Plants lose water through their leaves through a process called transpiration. This water is lost through small opening in the leaves called stomata. Inside the leaf the air is near saturation, and the difference between air saturation and leaf saturation causes the plant to lose moisture due to diffusion. The plant can control the loss of water by opening and closing the stomata. The loss of water vapor from plants can be calculated from a resistance law, where the difference in saturation between the interior of the leaf and the atmosphere is the forcing term, and the canopy stomatal resistance is the resisting term.
The canopy stomatal resistance values entered in GSSHA must represent the resistance of the canopy for an entire grid cell. The canopy resistance is affected by coverage, time of day, and the type and condition of plants in the cell. Greater leaf coverage means lower resistance values. In GSSHA, noontime canopy resistance values are entered. Canopy resistance has a strong diurnal variation and the GSSHA model corrects the noontime canopy resistance for the time of day. Although stomatal resistances are not commonly available for mixed-vegetation types, data are available for a variety of single vegetation types (e.g. Szeicz and Long, (1969) for grass; Stewart and Thom (1973) for pine forest; Allen et al. (1989) for clipped grass and alfalfa). Noontime values of canopy resistance (s m-1) for different types of plant under different conditions are listed in Table 12.
| Vegetation Type | Canopy Resistance at Noon (s/m) |
|---|---|
| Cotton fielda | ~ 17 |
| Coniferous forest (Spruce)a | ~ 100 |
| Coniferous forest (Hemlock)a | ~ 150 |
| Coniferous forest (Pine, March)b | ~ 140 |
| Coniferous forest (Pine, June)b | ~ 120 |
| Coniferous forest (Pine, September/October)b | ~ 123 |
| Prairie grasslands (late July)c | ~ 100 |
| Prairie grasslands (mid September)c | ~ 500 |
| Irrigated short grass cropd | ~ 86 |
| Unirrigated barleyd | ~ 43 |
Table 12 - Canopy Stomatal Resistance Notes: aPielke (1984); bGash and Stewart (1975), cMonteith (1975); and dSceicz and Long (1969).
The Penman-Monteith equation has been found to be very sensitive to the value of canopy resistance. As pointed out by Lemeur and Zhang (1990), a 10% error in canopy resistance will result in a 10% error in the estimated evapo-transpiration. Senarath et al (2000) found that the discharges calculated during long-term simulations with CASC2D were also sensitive to the canopy resistance.
In the northern hemisphere temperate zone ET is subject to strong seasonal variations. ET is dependent on both climatic conditions and the vegetative cover. The seasonal variability of climatic conditions is reflected in the model with the hourly hydrometeorological inputs (Senarath et al., 2000). Vegetative cover is represented with simple land use/land cover indexes, such as forest, pasture, etc. Seasonal changes in vegetation cover are best simulated with plant growth models. Comprehensive plant growth models, such as SWAT (Arnold et al., 1999), and hydrologic models that include comprehensive plant growth models, TOPOG_IRM (Dawes et al., 1997) require extensive information on plant communities and growing conditions. Such detailed data are not routinely available.
Senarath et al. (2000) determined that of the ET parameters used in the Penman-Monteith equation, evapo-transpiration is most sensitive to the value of canopy resistance, and is quite insensitive to the other ET parameters. Leaf area and canopy resistance can vary by as much as several hundred percent during the year for crops, grasses, and deciduous forest in temperate regions (Monteith, 1975; Doorenbos and Pruitt, 1977; Federer and Lash, 1978). Based on this information, the canopy resistance was chosen as the vehicle to incorporate seasonal variability of ET in the GSSHA model.
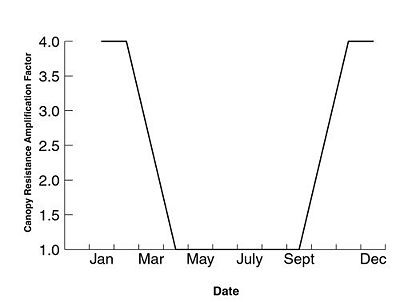
Mid-growing season values of canopy resistance are input as the starting point. For each month an amplification factor is used to represent the change in the canopy resistance related to plant growth. This mid-season value is then applied directly for the months of May through September. Thus, the amplification factor for May-September is 1.0. For the months November through February, the amplification factor is 4.0. This high factor relates to the death of crops, the browning of grasses and loss of leaves in deciduous trees. The months of March and October are considered transition months, and an amplification factor of 2.5 is used during these months. The timing of these events corresponds to values used for the transpirational leaf area of deciduous forest in North Carolina (Federer and Lash, 1978), though similar timing in conductance and ET is seen in other areas of the continental US (Nixon et al., 1972 for example). The implied assumptions of this simplistic approach, depicted in Figure 13, are then:
- Beginning of spring - at the end of March grasses begin to green, crops to sprout and trees leaf;
- Beginning of summer - by the first of May crops are near mature, and trees have full foliage;
- End of summer - by the beginning of October crops begin to die, grasses to brown and trees lose leaves; and,
- Fall/Winter - for the period November through February, plants are dormant and transpire little water to the atmosphere.
Use of this simple method at the Goodwin Creek Experimental Watershed (GCEW) in north Mississippi resulted in improved predictions of soil moistures and outlet discharge for periods outside the summer growing season (Downer, 2002a). The timing of seasonal changes should be adjusted to make the method applicable to climates different from that of southeast region of North America.
In GSSHA versions 5.x and higher, the above noted default values are applied for latitudes of 37 degrees and below. For latitudes greater than 37 degrees spring comes later and summer comes earlier; the four inflection points are April, July, September, and October. In versions 6.1 and above, these inflection points can be specified in the project file.
Seasonal variability of canopy resistance is selected by placing the SEASONAL_RS card in the project file along with the LONG_TERM card. In versions 6.1, and above, the inflection points on the curve can be specified by the user by using the cards SEASONAL_RS_SPRING SEASONAL_RS_SUMMER_START SEASONAL_RS_SUMMER_END and SEASONAL_RS_FALL. These cards are followed by the month, integer value, which the inflection point occurs. This capabilty allow users in the southern hemisphere or in regions of seasonal extremes to specify the timing on the inflection points. As shown in Figure 13, there is a linear transition between inflection points. ALL, or none, of the inflections points must be specified. For example, for the southern portion of the United States, below 37 latitude, the following cards describe the default conditions:
- LONG_TERM
- SEASONAL_RS
- SEASONAL_RS_SPRING 3
- SEASONAL_RS_SUMMER_START 5
- SEASONAL_RS_SUMMER_END 9
- SEASONAL_RS_FALL 10
9.1.4.3 Vegetation Height
The vegetation height is required to compute the aerodynamic resistance term in the calculation of turbulent diffusion. Vegetation heights are entered in meters. Sample values are listed in Table 13 (from Eagleson, 1970). The values may not be the representative, expected vegetation height-values of these vegetation/forest types.
| Vegetation / Forest Types | Sample Vegetation Height (cm) |
|---|---|
| Mown Grass | 1.5 - 4.5 |
| Alfalfa | 20 - 40 |
| Long Grass | 60 - 70 |
| Maize | 90 - 300 |
| Sugar Cane | 100 - 400 |
| Brush | 135 |
| Orange Orchard | 350 |
| Pine forest | 500 - 2700 |
| Deciduous forest | 1700 |
Table 13 - Sample values of vegetation height
9.1.4.4 Vegetation Transmission Coefficient
The plant canopy can prevent radiation from reaching the ground surface, reducing the amount of radiation available to heat the ground surface and produce evaporation. The vegetation transmission coefficient describes the fraction of light that penetrates the vegetation canopy and reaches the ground. Values can range between 0.0, total canopy blocking of sunlight, to 1.0, total light penetration on bare soil. Table 14 list measured values of canopy resistance for grass.
| Grass Height (cm) | Kt |
|---|---|
| 100 | 0.18 |
| 50 | 0.18 |
| 10 | 0.68 |
Table 14 - Vegetation transmission coefficient values for grass Notes: Data from O.G. Sutton, “Micrometeorology,” McGraw Hill, New York, 1953.
GSSHA User's Manual
- 9 Continuous
- 9.1 Computation of Evaporation and Evapo-transpiration
- 9.2 Computation of Soil Moisture
- 9.3 Hydrometeorological Data
- 9.4 Snowfall Accumulation and Melting
- 9.5 Sequence of Events During Long-Term Simulations