Model Construction:Determining an appropriate time-step
A good way to determine the appropriate time-step for a given problem is to conduct a temporal convergence study. Select from the study period a rainfall event of the highest rainfall intensity, or the one that produces the maximum discharge. Select a short time-step, 5 to 20 sec, and simulate the event. Write out the discharge hydrograph at small intervals, equal to the time-step. Increase the time-step and repeat. Continue increasing the time-step until the program crashes during execution. At this point, the upper limit of the time-step for your problem has been reached. Look at the hydrographs produced using the various time-steps. If the hydrograph begins to oscillate, normally near the peak, the time-step is too large. Eliminate any simulations that produce oscillations in the hydrograph.
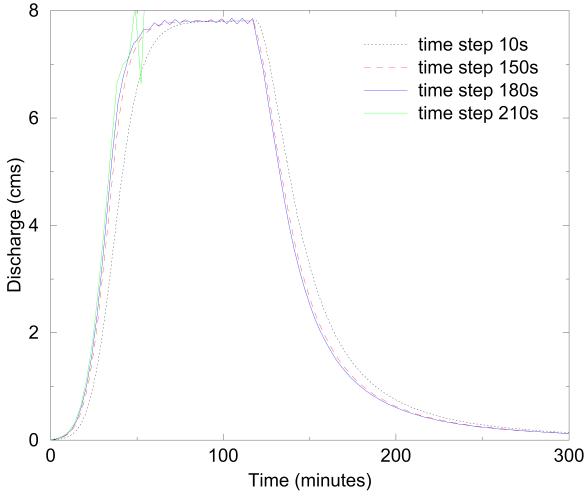
There should now be a set of hydrographs produced by various time-steps. As the time-step is increased, the hydrograph shape may begin to change. A primary theory of the finite difference method is that the model results converge on the solution as the time-step decreases. Therefore, the hydrograph with the smallest time should be treated as the “correct” answer, and the other hydrographs should be judged against it. A simple visual comparison of the hydrographs is usually sufficient. Figure 6 shows the hydrographs produced from a test case with time-steps of 10, 150, 180, and 210 sec. At 150 sec, the hydrograph is significantly shifted from the 10-sec simulation. At 180 sec, oscillations appear. At 210 sec, the oscillations cause the model to crash. All these time-steps are too large. The simulation time-step may also be judged by the peak discharge, time of peak, and discharge volume information from the summary file. To decrease wall clock execution time, select the largest time-step that produces results equal to, within an acceptable error level, the results with the smallest time-step.
Related Topics
GSSHA Wiki Main Page
Primer Main Page