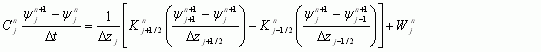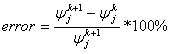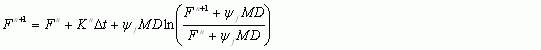Template:GUM7

 

7 - Infiltration

GSSHA User's Manual

Water ponded on overland flow plane cells will infiltrate into the soil as conditions permit. Infiltration is dependent upon soil hydraulic properties and antecedent moisture conditions, which may be affected by previous rainfall, run on, ET, and the location of the water table. In GSSHA, the unsaturated zone that controls infiltration may be simulated with a 1-D formulation of Richards’ equation (RE), which simulates infiltration, ET, and soil moisture movement in an integrated fashion. Infiltration may also be simulated using traditional Hortonian Green and Ampt (GA) (Green and Ampt, 1911) approaches which are simplifications of RE. There are three optional GA based methods to calculate infiltration for Hortonian basins: 1) traditional GA infiltration, 2) multi-layer GA, and 3) Green & Ampt infiltration with redistribution (GAR) (Ogden & Saghafian, 1997). The traditional GA and multi-layer GA approaches are used for single event rainfall when there are no significant periods of rainfall hiatus. The GAR approach is used when there are significant breaks in the rainfall, or for continuous simulations.

RE is a general equation and can be applied in any type of watershed or conditions. However, the simpler methods based on the GA equation are preferred when runoff is Hortonian, i.e. occurs due to infiltration excess, where the rainfall/run-on of water is greater than the possible infiltration rate. For fine textured soils the GAR method has been shown to closely mimic the RE solution (Ogden and Saghafian, 1997) and when applied in basins identified as Hortonian, the GAR method has been shown to produce results comparable with the RE (Downer and Ogden, 2003a).

However, when Hortonian flow is not the predominant stream flow producing mechanism, application of GA type models is ill advised and can result in erroneous results (Downer et al., 2002a). For cases where Hortonian flow is not the predominate process generating stream flow the RE should be used, and coupled with the saturated groundwater solution as appropriate. The saturated groundwater model can also be coupled with the GAR model. This represents a rather crude approximation of the actual processes, but has proven useful for numerous studies Eau Galle TN , JD31 TN. The advantage of this approach is a savings in computation time.

Representation of the soil column below each cell with Richards’ equation is presented. Formulation and application of the GA model is well described in other sources (i.e. Maidment, 1993) as well as the GAR method (Ogden and Saghafian, 1997). Formulation, solution, and application of the multi-layered GA model as applied in the GSSHA model is presented in Section 7.3.

7.1 Richards’ Equation

Detailed modeling of the soil water profile in the vadose, or unsaturated zone, is a key addition in the GSSHA model. It is this dynamic area that controls the flux of water between the surface and groundwater and partitions rainfall into infiltration, runoff, groundwater recharge and ET. The most rigorous way to model these complicated and integrated phenomena is to use Richards’ equation in the solution of the problem. While many have described RE as being infeasible for use in hydrologic predictions the equation has been successfully used in field scale and watershed scale models of soil moisture and runoff (Lappala et al., 1987; Hutson and Waggenet, 1989; Dawes and Hatton, 1993; Refsgaard and Storm, 1995; and others). Simpler methods, such as GA and GAR, which are approximations of RE do not provide detailed soil moisture profiles or simulate the movement of water from the groundwater to the unsaturated zone. Accurate representation of layered soils or soils with a water table difficult is also difficult with these approximations (Short et al., 1995). To simulate infiltration with Richards equation use the INF_RICHARDS option in the project file.

Processes in the unsaturated zone important to surface water hydrology, infiltration, ET, and groundwater recharge, are largely oriented in the vertical direction (Refsgaard and Storm, 1995). GSSHA solves the one-dimensional (vertical direction) head-based formulation of Richards’ equation

(14)

where:

C is the specific moisture capacity,

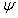is the soil capillary head (cm),

z is the vertical coordinate (downward positive) (cm),

t is time (hr),

K (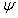) is the effective hydraulic conductivity (cm),

and W is a flux term added for sources and sinks (cm/hr).

The head-based formulation allows solution of Richards’ equation in both saturated and unsaturated conditions (Haverkamp et al. 1977). The head-based approach has been successfully implemented in the field scale unsaturated flow models VS2D (Lappala et al., 1987), LEACHM (Hutson and Wagenet, 1989), and SWAP (van Dam and Feddes, 2000) and in the surface water hydrology models TOPOG_IRM (Dawes and Hatton, 1993) and MIKE SHE (Refsgaard and Storm, 1995). With a head-based formulation, rainfall, evaporation and groundwater recharge can all be modeled without a change in variable. Known mass balance problems associated with solution of the head-based formula (Celia et al. 1987; Ross, 1990; Pan and Wierenga, 1995; Celia et al. 1990) have largely been eliminated by the development of new solution techniques (Kirkland et al., 1992; Rathfelder and Abriola, 1994; Pan and Wierenga, 1995).

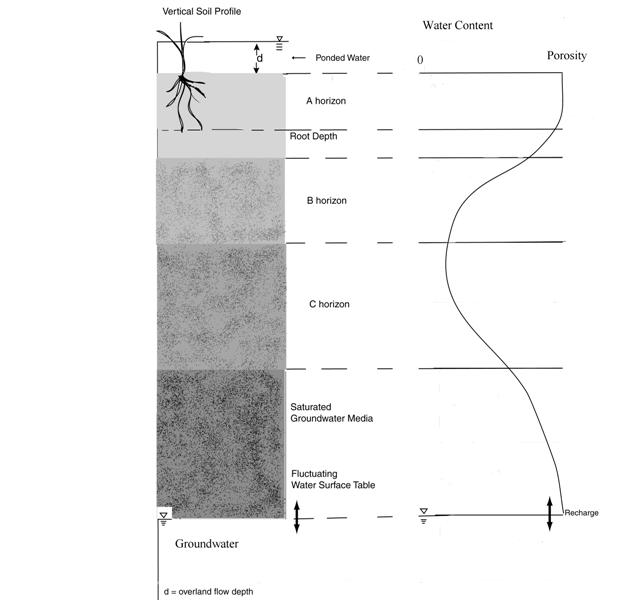
In GSSHA, RE is solved using an implicit finite difference approach, which maps directly to the overland flow finite difference grid. The soil column below each overland flow cell is sub-divided into multiple unsaturated zone cells, Figure 9.

Figure 9 - GSSHA representation of the unsaturated zone

A 1-D approximation of the unsaturated zone imposes some limitations on the application of the model. Lateral flow in the unsaturated zone may be significant for a perched water table that does not extend to the soil surface. Lateral flow of unsaturated water may also occur in the absence of a perched water table (Zaslavsky and Sinai, 1981). Lateral flow in the unsaturated zone under either saturated or unsaturated conditions is most significant for steep slopes. Solution of the multi-dimensional RE is difficult and the additional computational burden is not commonly justified if the purpose of the model is to simulate surface water hydrology. Aspect ratio problems are also avoided because of the 1-D formulation employed. Other conditions in the unsaturated zone that are not explicitly simulated are macro-pores and hysteresis.

7.1.1 Discretization

The soil column must be sub-divided into cells to numerically solve Richards’ equation. The discretization used in the GSSHA model is shown in Figure 9. The soil column is defined in three layers, namely A, B, and C horizons. The soil properties and discretization can vary in each layer. Any size cell can be used in the discretization, however, if very large cells are used the solution may be poor. As discussed in Downer (2002a) and Downer and Ogden (2002b), cells on the order of 1 cm are generally needed in the top 10 cm of soil to accurately model the infiltration process. If larger cells are used in dry soils a large volume of water must be added to the cell before significant infiltration can occur because the hydraulic conductivity will be very low. This can result in significant underestimation of infiltration, as discussed in Downer (2002a) and Downer and Ogden (2002b). The grid size for each soil in the SOIL_TYPE_MAP in each soil layer is specified in the SOIL_LAYER_INPUT_FILE or in the Mapping Table.

The solution scheme employed is implicit, central difference in space and forward difference in time, and is thus second order accurate in space, first order accurate in time. For j being the cell numbering scheme, increasing downward, such that j is the cell of interest, j-1 is the cell above, and j+1 is the cell below, and n represents the time level, Figure 9. The following discretization is used for non-boundary cells

(15)

where:

C = water capacity,

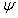= pressure head in the cell (cm),

K = hydraulic conductivity in the cell (cm/hr),

W = source term (cm/hr),

Δt = time step (hr), and

Δz = grid size (cm).

Values for variables represented between cells, or at the cell interface, are represented by j-1/2 and j+1/2 for the interfaces above and below, respectively. Inter-nodal distances, Δz_j-1\2, Δz_j+1\2, are defined as the distance between the center of cells j and j-1 and j and j+1, respectively, computed as:

(16)

Inter-cell hydraulic conductivities may be calculated two ways, an arithmetic weighting of the values or a geometric average. The inter-cell hydraulic conductivity weighting method is selected with the RICHARDS_K_OPTION project card with the argument being either ARITHMETIC or GEOMETRIC; the default is ARITHMETIC. In using the arithmetic weighting, a weighting factor, , is used to determine how much weight is placed on upper and lower cells. The value of is specified with the RICHARDS_WEIGHT project card; the default value is 1.0. If α = 1, then only the value from the j-1 cell is used; this is commonly referred to as backwards difference, or upwinding. If α = 0 only the j+1 value is used. This is commonly referred to as forward difference, or downwinding. If α is 0.5 then equal weight is applied to both the j-1 and j+1 cells. Lappala (1981) recommends that backward difference be used for modeling the infiltration process. The geometric average is best when there are large changes in the hydraulic conductivity between cells and is generally applicable in all situations.

7.1.2 Non-linear Coefficients

In Richards’ equation, hydraulic conductivity and water capacity values are dependent on the water content of the cell. The method to describe these relationships must be specified with the RICHARDS_C_OPTION project card. The possible arguments are BROOKS for the Brooks and Corey method (1964) and HAVERCAMP for the Havercamp method (Havercamp et al., 1977). The Brooks and Corey method (1964) as extended by Hutson and Cass (1987) may be used to estimate relative hydraulic conductivity from the soil pressure head as:

if < _b (17)

and if > _b K_r = 1.0 if

where: K_r is the relative hydraulic conductivity, _b is the air entry or bubbling pressure, and λ is the pore-size distribution index, which is the inverse of the ratio of the length of flow path through the soil matrix to the straight line length.

With the Havercamp method (Havercamp et al., 1977) as modified by Lappala et al. (1987) the relative hydraulic conductivity is calculated as:

(18)

where: A and B are parameters fitted to laboratory determinations of hydraulic conductivity at different soil pressure heads.

The water capacity C is also dependent on the pressure head . Water capacity is defined as the change in moisture with respect to head . For Brooks and Corey if < b the relationship between moisture content and head is expressed as

(19)

where: , θ is the moisture content, θ_r is the residual saturation, and θs is the saturated moisture content, or porosity. Rearranging and taking the derivative with respect to head yields

(20)

In the original formulation of Brooks and Corey, if > b, θ = s and C=0. This formulation permits changes in pressure head without a resulting change in water content for pressures greater than the bubbling pressure. Hutson and Cass (1987) extended the Brooks and Corey equation into the wet region where > b using the following formulation

(21)

where: , and θ_c is the critical moisture content, the moisture content where the curve changes from the standard Brooks and Corey curve to the modified curve of Hutson and Cass. The critical moisture content is defined as with the corresponding critical pressure head:

(22)

The moisture content can then be represented as

(23)

And, the water capacity is found by taking the derivative of the above equation.

(24)

For the Havercamp equations the relationship between the water content and the pressure head is

(25)

where: α and β are fitted parameters. According to Lappala (1981) the form of the equation can be expressed as:

(26)

Differentiating with respect to pressure yields the water capacity

(27)

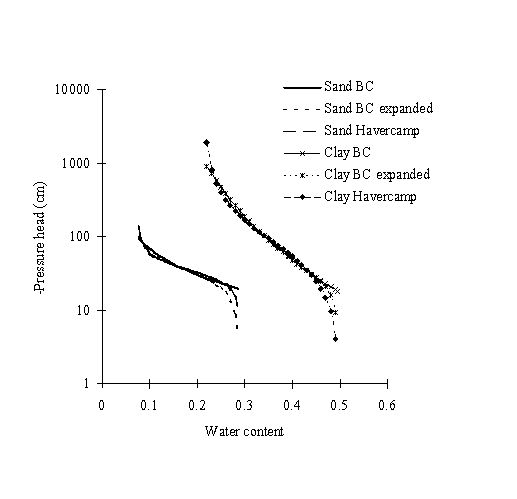
The relationship between soil moisture and suction head as represented by the different methods is shown in Figure 10.

Figure 10 – Water retention curves (BC – Brooks and Corey).

7.1.3 Evapo-transpiration Source Term

During long-term simulations potential evapo-transpiration (PET) is calculated by either the Penman Monteith (Monteith, 1965; 1981) or Deardorff (1977; 1978) equations and is applied to each soil column below the overland flow plane. Any water ponded on the surface of the overland flow cell is reduced up to amount of the PET. Any remaining PET demand is applied to cells in the unsaturated zone down to the specified root depth (Figure 9). The actual evapo-transpiration (AET) is distributed over the cells in the specified root zone in proportion to the size of each cell. The AET is computed from the PET by adjusting the PET for the soil moisture in each cell. AET depends on the soil moisture, hydraulic properties of the soil and plant characteristics. At water contents at or above the field capacity (θ_fc) there is no stress on plants and AET is equal to PET (Shuttelworth, 1993; Dingman, 1994). The field capacity is the water content at which the suction pressure prevents gravity drainage of the soil. Field capacity is not an actually physically measurable quantity and there are many descriptions of the conditions that correspond to the concept of field capacity. At water contents below the wilting point, θ_wq, plant transpiration ceases and plants wilt (Dingman, 1994), and AET is zero. At intermediate points AET will depend on PET and the water content. Many relationships to relate AET to PET have been suggested (Dyck, 1983). In GSSHA AET is calculated from PET for water contents greater than the wilting point using the relationship

(28)

The appropriate equation depends on vegetation, climate, and soil type. If the exponent, P, is 1 the relationship is linear, above 1 the curve is convex, and below 1 concave. Currently P is set to 1.0. Future versions will allow the power to be specified by the user to reflect the local conditions. The AET for each cell is added to the source term, W, for that cell in the RE solution.

7.1.4 Upper Boundary Condition

The upper boundary condition varies depending on the condition of the top cell: specified flux for no surface ponding, and specified pressure (head) when infiltration excess results in surface ponding. The first cell in the column, j=0 (Figure 9), is located above the ground surface, and a pressure is always specified for this cell. For a flux boundary condition, the pressure in the top cell is zero and the flux is added to cells via the source term, W. For a head boundary the pressure in the top cell is equal to the depth of ponded water. The typical sequence of events is described below.

At the beginning of simulations and at times between rainfall events there is typically no ponded water on the overland flow plane. The upper boundary condition for the unsaturated zone is a negative flux, equal to the AET of the top cell, cell 1 in Figure 9. When rainfall, runoff or some other source of water is added to the overland flow cell a flux boundary condition is initially specified for the RE solution. A flux equal to the depth of ponded water divided by the current time step is added to the source term, W, of the first non-boundary cell, cell 1 in Figure 9. New heads are calculated with this assumed flux. These heads are used to compute the inter-cell fluxes. The computed flux in cell 1 is compared to the source term. If the calculated flux is less than the specified (assumed) flux, then all the water cannot infiltrate into the soil column during the current time step. In this case, water ponds on the soil surface and the upper boundary is changed to a specified head, the head being the depth of ponded water. Heads are re-computed using the head boundary. To save computation time, the upper boundary condition remains a specified head until the overland flow cell becomes dry. At this point the boundary condition changes back to a specified flux, and remains a specified flux until infiltration capacity of the soil column is again exceeded. Water that enters the top cell is infiltration. Any water that does not infiltrate can become runoff or direct ET (DET).

As discussed in Downer (2002a) and Downer and Ogden (2002b), the assignment of the hydraulic conductivity at the ground surface, K_1/2 between j=0 and j=1 (Figure 9), has important implications in determining infiltration, infiltration excess, and ET. Three methods, specified with the RICHARDS_UPPER_OPTION project card and the appropriate argument, can be used to compute the hydraulic conductivity at the ground surface. The default option, NORMAL, is to use the cell-centered value of hydraulic conductivity in cell 1 (Figure 9). The cell-centered value of hydraulic conductivity is always used for a flux boundary condition. If the soil surface boundary condition is a head, hydraulic conductivity at the soil surface may be assumed to be the saturation value, selected by using the GREEN_AMPT argument, or an average of the saturation value and the cell-centered value, selected with the AVERAGE argument. The assumption is that there is always a very thin layer of saturated material at the soil surface any time water ponds. Either method results in increased infiltration compared to using the cell-centered value of hydraulic conductivity. As discussed in Downer (2002a) and Downer and Ogden (2002b), testing at two watersheds indicated either alternative method allows the use of larger cell sizes in the unsaturated zone without seriously affecting calculated hydrologic fluxes.

7.1.5 Lower Boundary Condition

Three different lower boundary conditions can be specified. When the groundwater table is far from the ground surface the lower boundary condition is a zero head gradient. Water entering the N-1 cell in the soil column exits at the incoming rate (Figure 9). This boundary condition is valid when the water table is so deep that its effect on processes in the upper soil column is negligible, and is the default option when a WATER_TABLE is not specified by the user. The lower boundary can also be a fixed water table, specified with the WATER_TABLE project card that specifies the name of a map containing starting groundwater elevations. When a fixed water table is simulated the top of the last cell, N, is just at the surface of the saturated groundwater (Figure 9). The pressure at the top of the cell is zero, and the pressure at cell’s center is positive, calculated as 0.5ΔZ_N (Figure 9). This groundwater boundary fluctuates when saturated groundwater is simulated. For a moving water table, the size of the last non-boundary cell, N-1, and the number of cells, N, changes as the water table rises and falls (Figure 9). A moving water table is specified by using the GW_SIMULATION card in the project file, and then supplying the required saturated groundwater inputs.

The unsaturated zone does not include the saturated zone. The flux between the saturated and unsaturated zones is calculated as part of the overall unsaturated solution. This separation of the saturated and unsaturated zones helps in determining mass balance errors and maintaining mass balance in both the saturated and unsaturated zones because water is either in one zone or the other. When water crosses the boundary between the saturated and unsaturated zones it is removed from one zone and placed in the other. Mass balance errors can occur for a variety of reasons including: model formulation, spatial and temporal discretization used, solution technique, and abrupt changes in material properties. In GSSHA the mass balance for each compartment, overland, stream, unsaturated, saturated, are calculated independently and integrated to compute an overall mass balance. Mass balance errors in any compartment may be controlled by reducing time steps or increasing stability criteria, as needed. The methods used to link the saturated and unsaturated zones are further described in later sections.

7.1.6 Solution

Richards’ equation is highly non-linear because both the water capacity and the hydraulic conductivity depend on the pressure, or water content, of the soil. Numerical solution of RE requires some type of linearization. In GSSHA the RE is linearized by making the water capacity and inter-cell hydraulic conductivity constant during each time step. With flux updating of the heads, as described by Kirkland et al. (1992), this provides a stable, accurate, and mass conserving solution for most conditions.

For N cells including the upper and lower boundary cells, N-2 equations are needed. The well-known Thomas algorithm (Thomas, 1949) is efficient for solution of the resulting tri-diagonal matrix. After solving for heads in each cell, flux updating (Kirkland et al., 1992) synchronizes the heads and soil moistures, and improves the mass balance. Fluxes (cm hr-1) across the top face of each cell, f_j-1/2, are computed as:

(29)

These are used to compute the change in water content of each cell as

(30)

The new water content is

(31)

Once the water content in each cell is updated, pressure heads in each cell are calculated based on the head-moisture content relationship and used in the next time step. Kirkland (1991) found it necessary to restrict flux updating to cells that were both unsaturated and not immediately adjacent to saturated cells. Testing by the authors confirms this needed restriction. The reason for this requirement is that in saturated cells, head changes can occur without a change in water content. This deficiency in the formulation can cause errors in the solution and the mass balance. In this case, iterating on K_r and C can produce substantial improvements in accuracy and mass balance.

The maximum number of iterations is specified by the user using the RICHARDS_ITERMAX project card, the default being one. While iterating on the hydraulic conductivity and water capacity will almost always improve the solution and mass balance to some extent, iterating is particularly useful anytime there are saturated cells in the unsaturated zone. Cells can become saturated when large changes in material properties exist between adjacent layers, when the upper boundary condition is a head, and when the saturated groundwater is rapidly rising. Experience indicates that when the top boundary is the head condition, the accuracy and mass balance are always improved by iterating on the non-linear coefficients. When the top boundary condition is a head the maximum number of iterations changes from the default to five, unless the user has specified more iterations.

Picard iterations (Celia et al., 1990) are used anytime the user specifies iterations or the upper boundary condition is a head. Heads at the n+1 time level are first calculated using values of K_r and C from the n time level. Water contents are calculated based on the fluxes, and heads are updated based on the water contents. K_r and C are then calculated based on the updated values of head and water content. The water contents and heads are set back to the n time level values and K_rⁿ⁺¹ and Cⁿ⁺¹ are used to compute values of head at the n+1 time level. The procedure is repeated until the convergence criterion is met or the maximum number of iterations is reached. The convergence criterion is applied independently to each soil column. The convergence criterion is the difference in head between iterations. The error is adjusted for the head in each cell because the error is most important for wet cells, where a small absolute error in head can cause a large error in the solution. The error for each cell is expressed as

(32)

where k expresses the iteration number, which should not be confused with n, which represents the time level. Iterations for a particular soil column cease once the maximum change in head is less than 1 mm.

7.1.7 Time Step Limitation

Because the discretization is implicit there is no inherent stability criteria for the scheme. However, a time step limitation is desirable to keep the scheme accurate and mass conserving. The time step limitation in GSSHA is adapted from Belmans (1983). The time step is limited such that a maximum change in water content, Δθ_allow, is not exceeded. If the maximum change in water content in any cell, Δθ_max, exceeds Δθ_allow the time step is reduced so that an exceedance during the next time step is not likely. The following limitation is used

(33)

The maximum allowable change in water content is specified by the user, with a suggested range of 0.002 to 0.03 (Belmans, 1983). Smaller limitations will result in longer simulation times. In GSSHA each soil column has its own time step limitation computation. This can greatly increase the speed of the model when rapid changes in water content occur in only a few soil columns. In this case, Δt for these few soil columns may be very small while Δt for the bulk of the soil columns in the watershed is still very large in comparison. The time step is limited by specifying the maximum water content change allowable with the RICHARDS_DTHETA_MAX project card; the default value is 0.025.

7.2 Green and Ampt (GA)

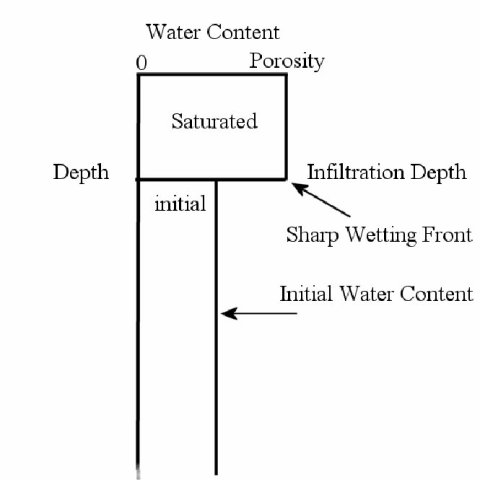
The Green-Ampt (GA) equation, developed for infiltration into uniform soils, has proven very useful in the field of hydrologic engineering. In the GA model water is assumed to enter the soil as a sharp (completely saturated) wetting front. The soil is assumed to homgeneous and infinite, with no restrictions due to the water table. The water can be thought of as entering the soil as a piston, shown in the figure below.

GA Infiltration Model

The GA method is selected by placing the GREEN_AMPT card in the project file. Four soil hydraulic parameters are needed for modeling the infiltration process using the G&A technique:

• GA hydraulic conductivity, K_ga (cm/h), half the saturated hydraulic conductivity K_s
• GA wetting front suction head, Φ_f (cm),
• effective porosity, θ_e,
• and initial soil moisture content, θ_i.

These values may be assigned by using the Mapping Table and an index map or with four GRASS ASCII maps. If using the Mapping Table and an index map the MAPPING_TABLE card is placed in the project file. The MOISTURE card is used with no argument. If using the GRASS ASCII maps to assign values to every cell in the watershed the CONDUCTIVITY, CAPILLARY, POROSITY, and MOISTURE cards are used to specify the GRASS ASCII map names as arguments. Assignment of parameters for all infiltration methods is discussed in Section 7.5.

7.3 Multi-layer Green and Ampt

While the basic Green and Ampt model has been proven effective for modeling infiltration into soils, several important common natural phenomena cause the assumption of a vertically uniform soil to be overly restrictive. Conditions such as layered soils, non-uniform initial soil moistures, surface crust, lenses, and high water tables all violate this basic assumption, yet are routinely encountered in the field. Therefore it becomes necessary to deal with these situations in some manner. The method used can have significant, if not overwhelming, effects on the hydrograph produced. This section discusses a methodology to incorporate a three layered soil profile into the GSSHA hydrologic model using Green-Ampt infiltration. Layering in soil may also be simulated with the Richards’ equation, Section 7.1.

In GSSHA v5 and above, the multi-layer GA model can be used in continuous mode, as well as with groundwater and in simulated constituent transport, including soils.

7.3.1 Layered Soils

In nature, layered soils are the norm rather than the exception. Everyone is familiar with the three layer soil system consisting of a top, A, middle, B, and bottom, C, horizon (Figure 9). Typically, soils in the A horizon are loose and high in organic material. High biological activity increases the porosity and hydraulic conductivity of soils in this layer. Soils in the B horizon are typically less permeable, with lower organic content and reduced biological activity. Soils in the C and lower horizons tend to be even less permeable, with minimal biological activity. What is found in the field could vary greatly from this simple model. Erosion and sedimentation, both recent and in geologic time frames, can cause very different layering effects. This can result in layers that become more porous with depth, or alternating porous and impermeable layers. Also, thin impermeable surface crusts can exist where compaction, raindrop impact or tillage occurs.

Regardless of the layering, when a wetting front moves from one layer to the next, the infiltration rate will be reduced. This is true regardless of the orientation of the layering. If a wetting front moves from a more porous to a less porous layer, the infiltration is reduced due to the reduced hydraulic conductivity. If the wetting front moves from a less porous layer to a more porous layer, the reduced wetting front suction causes the reduction in the infiltration rate. If the soils making up the lower layers are much coarser than the top layers, the wetting front may become unstable, and infiltration will be greatly reduced.

In a single layer infiltration model, the effect of layering must be addressed in some manner. Two possible approaches are: 1) use the properties of the top soil to represent the entire column, or 2) use some type of average values based on the depths of the layers.

7.3.2 Varying Moisture Contents

Soils do not have to be layered to cause problems with the Green-Ampt assumption of uniform soil properties. Soil moisture can also vary with depth. The variation in soil moistures with depth could be caused by layering or due to other reasons, such as interaction with the ground water table. In the latter case, the soil will tend to be driest at the surface and saturated near the water table. During periods of evaporation, the soil moisture content may vary considerably with depth. This type of condition can be roughly approximated with the three soil layer model, where the only parameter that changes through the layers is the initial soil moisture.

7.3.3 Model Formulation

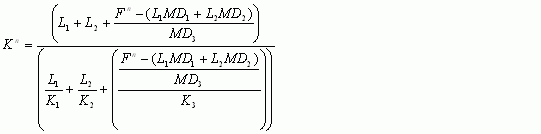
For GA infiltration in GSSHA, infiltration occurs in what is assumed to a uniform soil profile with constant hydraulic parameters and initial soil moisture throughout the profile. The Green-Ampt routine has been expanded to allow for three different soil layers to be modeled. These layers can be of any thickness and hydraulic parameters. The assumption of a sharp wetting front still applies. As the wetting front crosses the layers there is assumed to be an instantaneous change in the initial moisture, porosity, and wetting front suction head. However, the effective hydraulic conductivity is calculated at each time step based on the depth of the leading edge of the wetting front. The hydraulic conductivity, K (cm/hr), is calculated as the harmonic mean of the wetted layers. While the front is contained in the first layer, the hydraulic conductivity at any time n, K_n, is equal to K₁, the hydraulic conductivity of the A soil horizon.

After the wetting front passes into the second layer, the hydraulic conductivity is defined as:

(34)

where:

L₁=thickness of the A horizon (cm),

L₂=thickness of the B horizon (cm),

MD₁=moisture deficit of the A horizon (dimensionless),

MD₂=moisture content of the B horizon (dimensionless),

K₁=saturated hydraulic conductivity of the A horizon (cm/hr),

K₂=saturated hydraulic conductivity of the B horizon (cm/hr), and

Fⁿ= cumulative infiltration at the n time level (cm).

The moisture content MD is defined as the effective porosity θ_s minus the initial moisture content θ_i.

When the wetting front reaches the third layer, the effective hydraulic conductivity becomes:

(35)

where MD₃ (cm), and K₃ (cm/hr) are the moisture content and hydraulic conductivity, respectively, of the third soil layer.

Therefore the change in effective hydraulic conductivity is gradual, as would be expected in nature. The soil is assumed to be saturated at all points behind the wetting front.

The cumulative infiltration at the n+1 time level is (Adapted from Chow et al., 1988)

(36)

where: _ƒ, the wetting front suction head, and MD are for the layer containing the leading edge of the wetting front. This equation is solved iteratively by the Newton Raphson method. Once the cumulative infiltration is determined the infiltration rate, ƒ(cm/hr) is calculated by

(37)

Actually, for this method the calculation of the effective hydraulic conductivity lags the calculation of the infiltration by one time step. However, since the time steps for GSSHA are small, on the order of 1 minute, this should present minimal concern, because the hydraulic conductivity will change very little over such a short period.

In the case where rainfall rate is limiting, the cumulative infiltration is calculated as

(38)

where: dn+1 is the depth of water ponded on top of cell before infiltration is calculated.

The infiltration rate is then

(39)

7.3.4 Inputs

The multi-layered GA input represents an intermediate step in transforming from a map based input system to an index map and table based input system. The multi-layer GA approach is selected by placing the INF_LAYERED_SOIL card in the project file. Multi-layer GA requires the same inputs as the traditional GA approach except that the information must be specified in a table for all three layers. The table is specified with the SOIL_LAYER_INPUT_FILE card. This table is referenced to an index map that contains a unique integer number, starting with 1, for each soil type in the watershed. This GRASS ASCII map is specified with the SOIL_TYPE_MAP project card. The soil layer input file contains the number of soils on the first line, followed by the soil number and parameter values for each soil in the table. Soil numbers should start with soil 1 and increase monotonically. Every soil number in the table should correspond to a number in the SOIL_TYPE_MAP.

In GSSHA version 5.0 and above, the multi-layer GA model has been modified to work in long term simulation mode. The multi-layer GA model can also be coupled to saturated groundwater, and can be using in contaminant modeling, including simulation of contaminants in the soil column. The input table for the multi-layer GA model reflect these changes.

As shown below, values in the table are separated by spaces or tabs, not commas:

Total # of Soils Maximum soil id in the SOIL_TYPE_MAP Soil # Ks1    λ1    Sf1    θe1    θf1    θwp 1     θr1    θi1    d1 Ks2    λ2    Sf2    θe2    θf2    θwp 2     θr2    θi2    d2 Ks3    λ3    Sf3    θe3    θf3    θwp 3     θr3    θi3

Where: Ks is the saturated soil hydraulic conductivity (cm hr^-1),
   λ is the pore distribution index,
   Sf is the moisture front suction head (cm),
   θ is the soil moisture (fraction of total): e - saturated, f - field capacity, wp - wilting point, r - residual, i - initial,
   and d is the layer depth (cm).
The numbered subscripts refer to the soil layer number, 1 – top layer, 2 – middle layer, 3 – bottom layer.

For a watershed with three soil types, soil one a uniform clay, soil two a uniform sand, and soil three a sand with an embedded clay layer, the table might look like:

3 3 1 0.06    0.165    30.0    0.475    0.4    0.272    0.09    0.4   10.0 0.06    0.165    30.0    0.475    0.4    0.272    0.09    0.4    30.0 0.06    0.165    30.0    0.475    0.4    0.272    0.09    0.4 2 23.46    0.694    7.26    0.437    0.15    0.033    0.02    0.15    10.0 23.46    0.694    7.26    0.437    0.15    0.033    0.02    0.15    50.0 23.46    0.694    7.26    0.437    0.15    0.033    0.02    0.15 3 23.46    0.694    7.26    0.437    0.15    0.033    0.02    0.15    50.0   0.06    0.165   30.0    0.475    0.40    0.272    0.09    0.4    10.0 23.46    0.694    7.26    0.437    0.15    0.033    0.02    0.15    50.0

The corresponding SOIL_TYPE_MAP would contain the integers 1, 2 and 3 corresponding to the locations of the soils 1, 2, and 3 in the SOIL_LAYER_INPUT_FILE.

Newer versions of GSSHA, 5.7 and above, support the multi layer inputs in the MAPPING_TABLE_FILE. For these versions the inputs can be included as stated above, or more effciently, included in the MAPPING_TABLE_FILE. In this case, the above inputs are put into the MULTI_LAYER_SOIL table, as shown below. The inputs and the format are the same as above. WMS v9.0 and above support this ability. The table below was developed with WMS v9.1. It should be noted that the term BUB_PRESS is actually the wetting front suction head Sf.

MULTI_LAYER_SOIL "hawaii_Soil_final" NUM_IDS 2 MAX_SOIL_ID 4 ID    DESCRIPTION1    DESCRIPTION2   HYD_COND    LAMBDA    BUB_PRESS    POROSITY   FIELD_CAPA    WILTING_PT    RESID_SAT    SOIL_MOIST   DEPTH 1         Impermeable       roof_road              0.000010       0.165000       12.00000      0.500000      0.400000      0.100000      0.090000      0.180000      10.0                                                                0.000010       0.165000       12.00000      0.400000      0.380000      0.100000      0.090000       0.180000      10.0                                                                 0.000010       0.165000      12.00000      0.400000      0.380000      0.100000      0.090000      0.180000 4          SiltyClay          Residential_field       0.113842       0.150000      29.22000      0.493900      0.375000      0.250000      0.020000      0.400000      50.0                                                                  0.0604         0.150000       29.22000      0.484000      0.375000      0.250000      0.020000      0.400000      158.0                                                                   18.76             0.150000      29.22000     0.500000      0.375000      0.250000      0.020000      0.410000

7.4 Green and Ampt with Redistribution (GAR)

The GAR method expands the capability of the GA method by redistributing soil moisture during periods of no- or low- intensity rainfall. This allows infiltration capacity to recover for the next burst of storm intensity, and makes the GAR method suitable for simulating multiple rainfall events in series. When using the GAR method, multiple wetting fronts occur as burst of rainfall occur. During rainfall haitus these fronts are redistributed to produce a new value of initial moisture for calculations during the next burst of rainfall, Fig 12.

This method is selected with the INF_REDIST card in the project file. The technique for hiatus and post-hiatus infiltration was developed by Ogden and Saghafian (1997), and is similar to the method developed by Smith et al. (1993).

The GAR technique requires three additional inputs to the four required for the GA method, residual saturation and pore-size distribution index (Brooks & Corey, 1964), and field capacity. These must be input with in the Mapping Table. Assignment of parameters is discussed in Section 7.5.

Ogden and Saghafian (1997) performed a comparison of the GAR approach against a numerical solution of RE on each of the 11 USDA soil textural classifications for two pulses of rainfall separated by a period of no rainfall. It is important to note that the traditional GA is invalid for this case, unless the period of no rainfall is long enough in duration for the soil moisture profile to equilibrate. These results and other analysis presented by Ogden and Saghafian (1997) indicate that the GAR approach is a reasonably good approximation to the numerical solution of RE for well-drained soils, subjected to multiple pulses of rainfall. The agreement between the two approaches is better for finer textured soils. Coarse textured soils dry faster at the surface because of moisture profile “bulging”. The GAR approach cannot predict this phenomena, and therefore, overpredicts near soil-surface water contents after rainfall.

Figure 12. GAR multiple wetting fronts in soil profile.

7.5 Parameter Estimates

It is best to use soil property and Green-Ampt infiltration parameters derived from field and laboratory measurements of infiltration on the study watershed. Even under controlled conditions hydraulic soil property measurements are very difficult. Hysteresis effects and the extremely non-linear behavior of soil water retention make it very difficult to uniquely identify soil infiltration parameters. Hydrologic studies seldom have budgets sufficient to determine the needed parameters in the field.

Considerable prior research has been performed to relate soil infiltration parameter values to textural classification. Some highly relevant references are Rawls and Brakensiek (1983) and (1985), and Rawls et al. (1982) and (1983). Table 9 summarizes Rawls and Brakensiek soil parameter estimates as a function of United States Department of Agriculture (USDA) textural classification. It is important to note that the values listed in Table 9 were derived from the geometric mean of tests on a large number of soil samples. Hydraulic conductivies for all GA based approaches are half of the saturated values listed in Table 9 (Rawls, et al., 1982). The variance of these values is large, indicating significant uncertainty or low correlation between textural classification and soil texture. However, these values are useful because they provide an initial estimate of infiltration parameters. The variances of the values in Table 9 are listed in the original papers, and are published in Maidment (1993).

USDA Textural Classification	Total Porosity/Saturation   θs   (cm3/cm3)	Effective Porosity/Saturation   θe   (cm3/cm3)	Field Capacity Saturation   θf   (cm3/cm3)	Wilting Point Saturation   θwp   (cm3/cm3)	Residual Saturation   θr   (cm3/cm3)	Bubbling Pressure Geometric Mean   b (cm)	Pore Size Distribution Arithmetic Mean   λ   (cm/cm)	Saturated Hydraulic Conductivity (multiply by 0.5 for GA methods)   Ks (cm/h)	Wetting Front Suction Head (Capillary Head)   ƒ (cm)
Sand	0.437	0.417	0.091	0.033	0.02	7.26	0.694	23.56	4.95
Loamy sand	0.437	0.401	0.125	0.055	0.035	8.69	0.553	5.98	6.13
Sandy loam	0.453	0.412	0.207	0.095	0.041	14.66	0.378	2.18	11.01
Loam	0.463	0.434	0.27	0.117	0.027	11.15	0.252	1.32	8.89
Silt loam	0.501	0.486	0.33	0.133	0.015	20.79	0.234	0.68	16.68
Sandy clay loam	0.398	0.330	0.255	0.148	0.068	28.08	0.319	0.30	21.85
Clay loam	0.464	0.390	0.318	0.197	0.075	25.89	0.242	0.20	20.88
Silty clay loam	0.471	0.432	0.366	0.208	0.040	32.56	0.177	0.20	27.30
Sandy clay	0.430	0.321	0.339	0.239	0.109	29.17	0.223	0.12	23.90
Silty clay	0.479	0.423	0.387	0.250	0.056	34.19	0.150	0.10	29.22
Clay	0.475	0.385	0.396	0.272	0.090	37.30	0.165	0.06	31.63

Table 9 - Rawls & Brakensiek soil parameter estimates.

In the table soil moistures θ, are listed for saturation (s), effective saturation (e), field capacity (f), wilting point (wp), and residual (r). These values are applicable for all approaches. These are followed by the bubbling pressure _b (used for RE), the pore distribution index (used for RE, GAR and multi-layer GA in continuous mode), saturated hydraulic conductivity K_s (used directly for RE, halved for all GA approaches), the wetting front suction head f (used for all GA approaches).

Standard practice in developing GSSHA models is to obtain digital soil textural classification data and use these data to develop an index map of soil types. Soil textural maps may be combined with land use or vegetation maps. Land use and vegetation can strongly influence soil hydraulic properties. The Mapping Table is used to assign initial parameters to the soil types in the index map. One or more of these parameters, typically K_s and f or _b, are used as calibration parameters. As discussed by Senarath et al (2000), calibration is best done using an automated calibration method, such as SCE (Duan et al, 1992), combined with long term simulations. The possible parameter values are bounded by the range found in literature values, unless other factors, such as land use or vegetation, dictate otherwise. The range of values may be narrowed by making field and laboratory measurements of parameters.

Impervious areas can be accounted for by modifying the infiltration parameters as described above, or the area available for infiltration into a cell can be adjusted by specifying the impervious fraction using the AREA_REDUCTION process and including an index map for impervious area. Include the AREA_REDUCTION card in the project file and an AREA_REDUCTION mapping table with the fraction impervious for each value in the associated index map. Also see the section on Mapping Tables.